如图, 是 的直径,点 ,点 在 上, , 与 相交于点 , 与 相切于点 ,与 延长线相交于点 .
(1)求证: .
(2)若 , ,求 的半径.

如图所示,小明家小区空地上有两颗笔直的树CD、EF.一天,他在A处测得树顶D的仰角∠DAC=30°,在B处测得树顶F的仰角∠FBE=45°,线段BF恰好经过树顶D.已知A、B两处的距离为2米,两棵树之间的距离CE=3米,A.B、C、E四点在一条直线上,求树EF的高度.(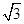 ≈1.7,
≈1.7,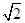 ≈1.4,结果保留一位小数)
≈1.4,结果保留一位小数)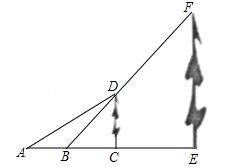
如图, 是等边三角形, ,动点 从点 出发,以 的速度沿 向点 匀速运动,过点 作 ,交折线 于点 ,以 为边作等边三角形 ,使点 , 在 异侧.设点 的运动时间为 , 与 重叠部分图形的面积为 .
(1) 的长为 (用含 的代数式表示).
(2)当点 落在边 上时,求 的值.
(3)求 关于 的函数解析式,并写出自变量 的取值范围.

小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)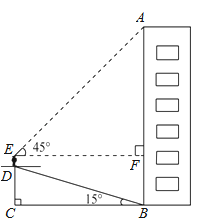
(1)求小华此时与地面的垂直距离CD的值;
(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.
如图, 为 的直径, 为 上一点, 是弧 的中点, 与 、 分别交于点 、 .
(1)求证: ;
(2)求证: ;
(3)若 ,求 的值.

能够完全重合的平行四边形纸片 和 按图①方式摆放,其中 , .点 , 分别在边 , 上, 与 相交于点 .
【探究】求证:四边形 是菱形.
【操作一】固定图①中的平行四边形纸片 ,将平行四边形纸片 绕着点 顺时针旋转一定的角度,使点 与点 重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .
【操作二】将图②中的平行四边形纸片 绕着点 继续顺时针旋转一定的角度,使点 与点 重合,连接 , ,如图③,若 ,则四边形 的面积为 .

小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: ,
, .结果保留整数)
.结果保留整数)
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
如图, 是 的直径, 与 相切于点 ,与 的延长线交于点 , 于点 .
(1)求证: ;
(2)若 , ,求 的半径.

如图①,在 中, , , .点 从点 出发,沿折线 以每秒5个单位长度的速度向点 运动,同时点 从点 出发,沿 以每秒2个单位长度的速度向点 运动,点 到达点 时,点 、 同时停止运动.当点 不与点 、 重合时,作点 关于直线 的对称点 ,连结 交 于点 ,连结 、 .设点 的运动时间为 秒.
(1)当点 与点 重合时,求 的值.
(2)用含 的代数式表示线段 的长.
(3)当 为锐角三角形时,求 的取值范围.
(4)如图②,取 的中点 ,连结 .当直线 与 的一条直角边平行时,直接写出 的值.

如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
.
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
如图,在矩形 中, , ,点 为边 上的一点(与 、 不重合),四边形 关于直线 的对称图形为四边形 ,延长 交 于点 ,记四边形 的面积为 .
(1)若 ,求 的值;
(2)设 ,求 关于 的函数表达式.

图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC′D′,最后折叠形成一条线段BD″.
(1)小床这样设计应用的数学原理是 .
(2)若AB:BC=1:4,则tan∠CAD的值是 .
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: ≈1.41,
≈1.41, ≈1.73.
≈1.73.