初中数学解直角三角形解答题

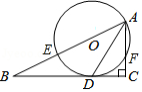
如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作直线DE垂直BC于F，且交BA的延长线于点E．

（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若cos∠BAC=，⊙O的半径为6，求线段CD的长．

如图，在 $\odot O$中，直径 $\mathit{AB}$经过弦 $\mathit{CD}$的中点 $E$，点 $M$在 $\mathit{OD}$上， $\mathit{AM}$的延长线交 $\odot O$于点 $G$，交过 $D$的直线于 $F$， $\angle 1=\angle 2$，连接 $\mathit{BD}$与 $\mathit{CG}$交于点 $N$．

（1）求证： $\mathit{DF}$是 $\odot O$的切线；

（2）若点 $M$是 $\mathit{OD}$的中点， $\odot O$的半径为3， $\tan \angle \mathit{BOD}=2\sqrt{2}$，求 $\mathit{BN}$的长．

如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC为10m，测角仪的高度CD为1．5m，测得树顶A的仰角为33°．求树的高度AB．（参考数据：sin33°≈0．54，cos33°≈0．84，tan33°≈0．65）

如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC．过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点．

（1）求证：CF为⊙O的切线；
（2）若⊙O的半径为cm，弦BD的长为3cm，求CF的长．

在矩形中，为边上一点，把沿翻折，使点恰好落在边上的点．

（1）求证：；

（2）若，，求的长；

（3）若，记，，求的值．

如图，一堤坝的坡角∠ABC=60°，坡面长度AB=24米（图为横截面）．为了使堤坝更加牢固，需要改变堤坝的坡面，为使得坡面的坡角∠ADB=50°，则应将堤坝底端向外拓宽（BD）多少米？（结果精确到0．1米）（参考数据：≈1．73，sin50°≈0．77，cos50°≈0．64，tan50°≈1．20）

如图，已知 $\mathit{AB}$是 $\odot O$的直径，弦 $\mathit{CD}$与直径 $\mathit{AB}$相交于点 $F$．点 $E$在 $\odot O$外，作直线 $\mathit{AE}$，且 $\angle \mathit{EAC}=\angle D$．

（1）求证：直线 $\mathit{AE}$是 $\odot O$的切线．

（2）若 $\mathit{BC}=4$， $\cos \angle \mathit{BAD}=\frac{3}{4}$， $\mathit{CF}=\frac{10}{3}$，求 $\mathit{BF}$的长．

某海域有A、B、C三艘船正在捕鱼作业，C船突然出现故障，向A、B两船发出紧急求救信号，此时B船位于A船的北偏西47°方向，距A船26海里的海域，C船位于A船的北偏东58°方向，同时又位于B船的北偏东88°方向．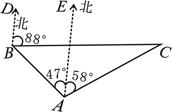

（1）求∠ABC的度数；
（2）A船以每小时40海里的速度前去救援，问多长时间能到出事地点．（结果精确到0．01小时）．
（参考数据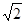：≈1．414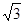，≈1．732）

如图，在 $\mathit{\Delta ABC}$中， $\angle B=90°$，点 $D$为 $\mathit{AC}$上一点，以 $\mathit{CD}$为直径的 $\odot O$交 $\mathit{AB}$于点 $E$，连接 $\mathit{CE}$，且 $\mathit{CE}$平分 $\angle \mathit{ACB}$．

（1）求证： $\mathit{AE}$是 $\odot O$的切线；

（2）连接 $\mathit{DE}$，若 $\angle A=30°$，求 $\frac{\mathit{BE}}{\mathit{DE}}$．

如图，为的直径，为上一点，与过点的直线互相垂直，垂足为，平分．

（1）求证：为的切线．

（2）若，，求的半径．

（1）如图1，4条直线l₁、l₂、l₃、l₄是一组平行线，相邻2条平行线的距离都是2cm，正方形ABCD的4个顶点A、B、C、D分别在l₁、l₃、l₄、l₂上，求该正方形的面积；
（2）如图2，把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中，恰好四个顶点都在横格线上，已知∠1=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0．60，cos36°≈0．80，tan36°≈0．75）

如图，在 $\mathit{\Delta ABC}$ 中， $\angle C=90°$ ， $\mathit{AD}$ 平分 $\angle \mathit{BAC}$ 交 $\mathit{BC}$ 于点 $D$ ，过点 $A$ 和点 $D$ 的圆，圆心 $O$ 在线段 $\mathit{AB}$ 上， $\odot O$ 交 $\mathit{AB}$ 于点 $E$ ，交 $\mathit{AC}$ 于点 $F$ ．

（1）判断 $\mathit{BC}$ 与 $\odot O$ 的位置关系，并说明理由；

（2）若 $\mathit{AD}=8$ ， $\mathit{AE}=10$ ，求 $\mathit{BD}$ 的长．

如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处正东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC等于多少米？

根据道路管理规定，在贺州某段笔直公路上行驶的车辆，限速40千米/时，已知交警测速点M到该公路A点的距离为米，∠MAB=45°，∠MBA=30°（如图所示），现有一辆汽车由A往B方向匀速行驶，测得此车从A点行驶到B点所用的时间为3秒．

（1）求测速点M到该公路的距离；
（2）通过计算判断此车是否超速．（参考数据：≈1．41，≈1．73，≈2．24）

化简求值（，其中．