我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
(1)求山坡高度;
(2)为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B 沿BC削进到E处,问BE至少是多少米(结果保留根号)?
如图1,滨海广场装有可利用风能、太阳能发电的风光互补环保路灯,灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米, ,且根据我市的地理位置设定太阳能板AB的倾斜角为
,且根据我市的地理位置设定太阳能板AB的倾斜角为 ,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍旋转,叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得
,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍旋转,叶片与太阳能板顶端A的最近距离不得少于0.5米,求灯杆OF至少要多高?(利用科学计算器可求得 ,
, ,
, ,结果保留两位小数)
,结果保留两位小数)
理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=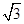 .tanD=tan15°=
.tanD=tan15°= =
=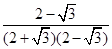 =
= .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=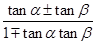 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=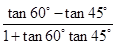 =
= =
= .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线 与双曲线
与双曲线 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是 上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于 上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
①当点P运动到 的中点P1时(如图二),求MN的长;
的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.
如图, 是坐标原点,矩形
是坐标原点,矩形 的顶点
的顶点 在
在 轴的正半轴上,点
轴的正半轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在边
在边 上,且点
上,且点 ,
, .
.
(1)填空: 的长为 ;
的长为 ;
(2)若 是
是 的中点,将过点
的中点,将过点 的直线
的直线 绕
绕 旋转,分别与直线
旋转,分别与直线 、
、 相交于点
相交于点 、
、 ,与直线
,与直线 相交于点
相交于点 ,连结
,连结 .
.
①设 点的纵坐标为
点的纵坐标为 .当
.当 ∽
∽ 时,求
时,求 的值;
的值;
②试问:在旋转的过程中,线段 与
与 能否相等?若能,请求出
能否相等?若能,请求出 的长;若不能,请说明理由.
的长;若不能,请说明理由.
如图,在▱ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将▱ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
(1)当点H与点C重合时.
①填空:点E到CD的距离是 ;
②求证:△BCE≌△GCF;
③求△CEF的面积;
(2)当点H落在射线BC上,且CH=1时,直线EH与直线CD交于点M,请直接写出△MEF的面积.
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
可证:AE⊥BF;
(1)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM,如图2,若AM和BF相交
于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
(2)将△BCF沿BF对折,得到△BPF,如图3,延长FP交BA的延长线于点Q,求sin∠BQP的值;
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
(1)求∠DAC的度数;
(2)求这棵大树原来的高度是多少米?(结果精确到个位,参考数据: ,
, ,
, )
)
已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.
(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.
①若CF=CD时,求sin∠CAB的值;
②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)
(本题满分14分,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分5分)
已知:如图, 是半圆
是半圆 的直径,弦
的直径,弦 ,动点
,动点 、
、 分别在线段
分别在线段 、
、 上,且
上,且 ,
, 的延长线与射线
的延长线与射线 相交于点
相交于点 、与弦
、与弦 相交于点
相交于点 (点
(点 与点
与点 、
、 不重合),
不重合), ,
, .设
.设 ,
, 的面积为
的面积为 .
.

(1)求证: ;
;
(2)求 关于
关于 的函数关系式,并写出它的定义域;
的函数关系式,并写出它的定义域;
(3)当 是直角三角形时,求线段
是直角三角形时,求线段 的长.
的长.
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)如图1,当∠ABE=45°,c=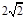 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠ABE=30°,c=4时,a= ,b= ;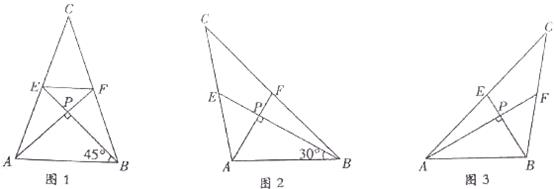
归纳证明
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=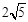 ,AB=3.求AF的长.
,AB=3.求AF的长.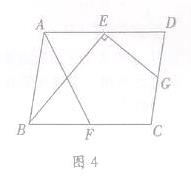
如图,以O为圆心的 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1) 的值为 ;
的值为 ;
(2)若OE与 交于点M,OC平分∠BOE,连接CM.求证:CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.求证:CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
2015年4月25日14时11分尼泊尔发生了8.1级大地震.山坡上有一棵与水平面垂直的大树,大地震过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示).已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4米.
(1)求∠DAC的度数;
(2)求这棵大树原来的高度是多少米?(结果精确到个位,参考数据: ,
, ,
, )
)
某水库大坝的横截面是如图所示的四边形BACD,期中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角 ,观测渔船N在俯角
,观测渔船N在俯角 ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度 .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为 ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据: )
)
如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.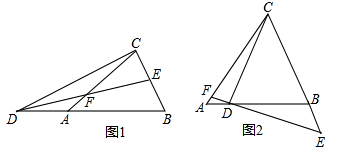
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).