如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
可证:AE⊥BF;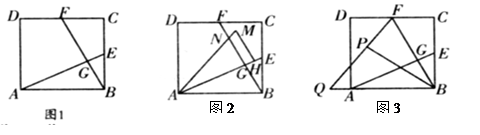
(1)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM,如图2,若AM和BF相交
于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
(2)将△BCF沿BF对折,得到△BPF,如图3,延长FP交BA的延长线于点Q,求sin∠BQP的值;
推荐套卷
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
可证:AE⊥BF;
(1)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM,如图2,若AM和BF相交
于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
(2)将△BCF沿BF对折,得到△BPF,如图3,延长FP交BA的延长线于点Q,求sin∠BQP的值;