湖北省武汉市青山区中考一模数学试卷
下面调查中,适合采用全面调查的事件是( )
| A.对全国中学生心理健康现状的调查 |
| B.对我市食品合格情况的调查 |
| C.对桂林电视台《桂林板路》收视率的调查 |
| D.对你所在的班级同学的身高情况的调查 |
下列运算中,正确的是( )
| A.x2+x4=x6 | B.2x+3y=5xy | C.x6÷x3=x2 | D.(x3)2=x6 |
已知,如图,E(-4,2),F(-1,-1).以O为位似中心,按比例尺1:2把△EFO缩小,点E的对应点)的坐标( )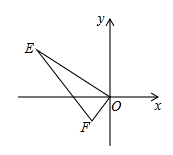
| A.(-2,1) |
| B.(2,-1) |
| C.(2,-1)或(-2,-1) |
| D.(-2,1)或(2,-1) |
来自某综合市场财务部的报告表明,商场2014年1-4月份的投资总额一共是2017万元,商场2014年第一季度每月利润统计图和2014年1-4月份利润率统计图如下(利润率=利润÷投资金额):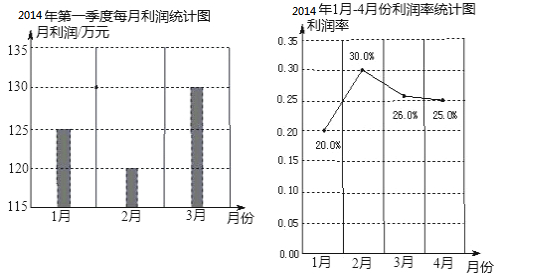
根据以上信息,下列判断不正确的是( )
| A.商场2014年第一季度中3月份投资金额最多 |
| B.商场2014年第一季度中2月份投资金额最少 |
| C.商场2014年4月份利润比2月份的利润高 |
| D.商场四个月的利润所组成的一组数据的中位数是124 |
用同样大小的黑色棋子按如图所示的规律摆放,则第100个图中有棋子 ( )
| A.300枚 | B.301枚 | C.303枚 | D.304枚 |
在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是( )
| A.1 | B.3 | C. |
D.2 |
环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为 .
、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时, 甲离终点还有 米.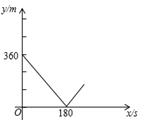
如图,B、D两点均在双曲线y= 上,BC垂直于y轴于点C,点D为AB的中点,点E在线段OC上,且CE=2OE,若△BDE的面积为7,则k的值为 .
上,BC垂直于y轴于点C,点D为AB的中点,点E在线段OC上,且CE=2OE,若△BDE的面积为7,则k的值为 .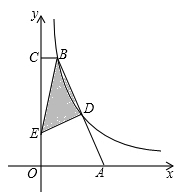
如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面 积为 .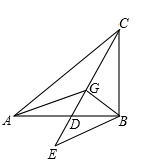
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题: 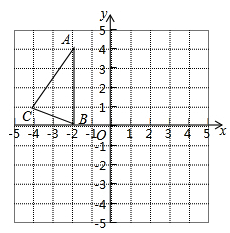
(1)请画出△A1B1C1;
(2)请直接写出点B2、C2的坐标;
(3)在△ABC、△A1B1C1、△A2B2C2中 ,△A2B2C2与 成中心对称,其对称中心的坐标为 .
商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.
(1)若他去买一瓶饮料,则他买到汁的概率是 ;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.
如图,AB是⊙O的直径,BC交⊙O于点D,E是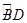 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB. 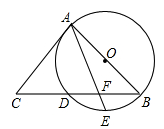
(1)求证:AC是⊙O的切线;
(2)若cosC=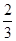 ,AC=6,求BF的长.
,AC=6,求BF的长.
某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
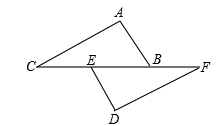
如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.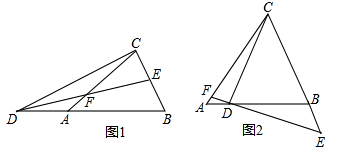
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).
已知在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0,且a,b,c为常数)的对称轴为:直线x=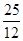 ,与x轴分别交于点A、点B,与y轴交于点C(0,
,与x轴分别交于点A、点B,与y轴交于点C(0,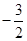 ),且过点(3,-5),D为x轴正半轴上的动点,E为y轴负半轴上的动点.
),且过点(3,-5),D为x轴正半轴上的动点,E为y轴负半轴上的动点.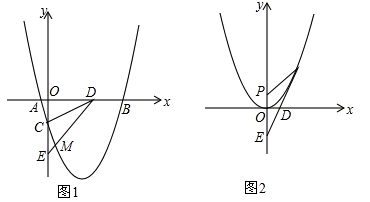
(1)求该抛物线的表达式;
(2)如图1,当点D为(3,0)时,DE交该抛物线于点M,若∠ADC=∠CDM,求点M的坐标;
(3)如图2,把(1)中抛物线平移使其顶点与原点重合,若直线ED与新抛物线仅有唯一交点Q时,y轴上是否存在一个定点P使PE=PQ?若存在,求出点P的坐标;若不存在,请说明理由.
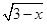 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )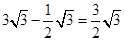
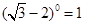

 粤公网安备 44130202000953号
粤公网安备 44130202000953号