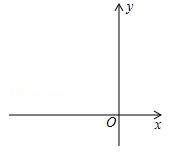
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),将△ABC绕原点O旋转180度得到△A1B1C1.平移△ABC得到△A2B2C2,使点A移动到点A2(0,2),结合所给的平面直角坐标系解答下列问题: 
(1)请画出△A1B1C1;
(2)请直接写出点B2、C2的坐标;
(3)在△ABC、△A1B1C1、△A2B2C2中 ,△A2B2C2与 成中心对称,其对称中心的坐标为 .
相关知识点
推荐套卷


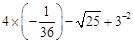 ;
;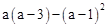 .
.
 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.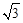 ,求m的值.
,求m的值. ,求此时BP的长度.
,求此时BP的长度.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号