[性质探究]
如图,在矩形 中,对角线 , 相交于点 , 平分 ,交 于点 .作 于点 ,分别交 , 于点 , .
(1)判断 的形状并说明理由.
(2)求证: .
[迁移应用]
(3)记 的面积为 , 的面积为 ,当 时,求 的值.
[拓展延伸]
(4)若 交射线 于点 ,[性质探究]中的其余条件不变,连结 ,当 的面积为矩形 面积的 时,请直接写出 的值.

定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

如图,在平面直角坐标系中,正方形 的两直角边分别在坐标轴的正半轴上,分别过 , 的中点 , 作 , 的平行线,相交于点 ,已知 .
(1)求证:四边形 为菱形.
(2)求四边形 的面积.
(3)若点 在 轴正半轴上(异于点 ,点 在 轴上,平面内是否存在点 ,使得以点 , , , 为顶点的四边形与四边形 相似?若存在,求点 的坐标;若不存在,试说明理由.

如图,已知 , 为 的两条直径,连接 , , 于点 ,点 是半径 的中点,连接 .
(1)设 的半径为1,若 ,求线段 的长.
(2)连接 , ,设 与 交于点 ,
①求证: .
②若 ,求 的度数.

如图1,已知四边形 是矩形,点 在 的延长线上, . 与 相交于点 ,与 相交于点 , .
(1)求证: ;
(2)若 ,求 的长;
(3)如图2,连接 ,求证: .

将正方形 的边 绕点 逆时针旋转至 ,记旋转角为 ,连接 ,过点 作 垂直于直线 ,垂足为点 ,连接 , .
(1)如图1,当 时, 的形状为 ,连接 ,可求出 的值为 ;
(2)当 且 时,
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点 , , , 为顶点的四边形是平行四边形时,请直接写出 的值.

抛物线 与 轴交于 、 两点,与 轴交于点 ,点 的坐标为 ,点 的坐标为 .点 为抛物线 上的一个动点.过点 作 轴于点 ,交直线 于点 .
(1)求 、 的值;
(2)设点 在抛物线 的对称轴上,当 的周长最小时,直接写出点 的坐标;
(3)在第一象限,是否存在点 ,使点 到直线 的距离是点 到直线 的距离的5倍?若存在,求出点 所有的坐标;若不存在,请说明理由.
如图1,在矩形 中, , ,点 , 分别为 , 的中点.
(1)求证:四边形 是矩形;
(2)如图2,点 是边 上一点, 交 于点 ,点 关于 的对称点为点 ,当点 落在线段 上时,则有 .请说明理由;
(3)如图3,若点 是射线 上一个动点,点 关于 的对称点为点 ,连接 , ,当 是等腰三角形时,求 的长.
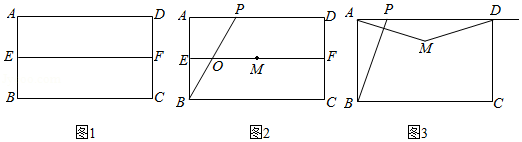
已知:如图,在菱形 中,点 、 分别在边 、 上, , 的延长线交 的延长线于点 , 的延长线交 的延长线于点 .
[小题1]求证: ;
[小题2]如果 ,求证: .
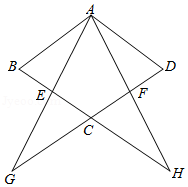
如图,在直角梯形 中, , , , , .
(1)求梯形 的面积;
(2)联结 ,求 的正切值.
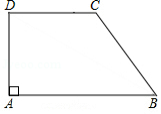
[小题1]求梯形 的面积;
[小题2]联结 ,求 的正切值.
综合与探究
如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 .直线 与抛物线交于 , 两点,与 轴交于点 ,点 的坐标为 .
(1)请直接写出 , 两点的坐标及直线 的函数表达式;
(2)若点 是抛物线上的点,点 的横坐标为 ,过点 作 轴,垂足为 . 与直线 交于点 ,当点 是线段 的三等分点时,求点 的坐标;
(3)若点 是 轴上的点,且 ,求点 的坐标.

某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积 , , 之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在 中, 为斜边,分别以 , , 为斜边向外侧作 , , ,若 ,则面积 , , 之间的关系式为 ;
推广验证
(2)如图3,在 中, 为斜边,分别以 , , 为边向外侧作任意 , , ,满足 , ,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形 中, , , , ,点 在 上, , ,求五边形 的面积.

如图,二次函数 的图象经过 , , 三点,以点 为位似中心,在 轴的右侧将 按相似比 放大,得到△ ,二次函数 的图象经过 , , 三点.
(1)画出△ ,试求二次函数 的表达式;
(2)点 在二次函数 的图象上, ,直线 与二次函数 的图象交于点 (异于点 .
①求点 的坐标(横、纵坐标均用含 的代数式表示)
②连接 ,若 ,求 的取值范围;
③当点 在第一象限内,过点 作 平行于 轴,与二次函数 的图象交于另一点 ,与二次函数 的图象交于点 , 在 的左侧),直线 与二次函数 的图象交于点 .△ △ ,则线段 的长度等于 .

如图1,四边形 是矩形,点 的坐标为 ,点 的坐标为 ,点 从点 出发,沿 以每秒1个单位长度的速度向点 运动,同时点 从点 出发,沿 以每秒2个单位长度的速度向点 运动,当点 与点 重合时运动停止.设运动时间为 秒.
(1)当 时,线段 的中点坐标为 ;
(2)当 与 相似时,求 的值;
(3)当 时,抛物线 经过 , 两点,与 轴交于点 ,抛物线的顶点为 ,如图2所示,问该抛物线上是否存在点 ,使 ?若存在,求出所有满足条件的 的坐标;若不存在,说明理由.
