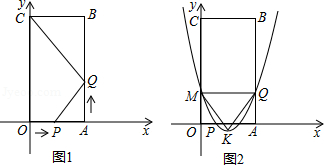
如图1，四边形 是矩形，点 的坐标为 ，点 的坐标为 ，点 从点 出发，沿 以每秒1个单位长度的速度向点 运动，同时点 从点 出发，沿 以每秒2个单位长度的速度向点 运动，当点 与点 重合时运动停止．设运动时间为 秒．
（1）当 时，线段 的中点坐标为 ；
（2）当 与 相似时，求 的值；
（3）当 时，抛物线 经过 ， 两点，与 轴交于点 ，抛物线的顶点为 ，如图2所示，问该抛物线上是否存在点 ，使 ？若存在，求出所有满足条件的 的坐标；若不存在，说明理由．
如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．
（1）求证：DE平分∠BDC；
（2）若点M在DE上，且DC=DM，求证：ME=BD．
已知，在△ABC中，AB=AC．过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ，直线a交BC边于点P（点P不与点B、点C重合），△BMN的边MN始终在直线a上（点M在点N的上方），且BM=BN，连接CN．
（1）当∠BAC=∠MBN=90°时，
①如图a，当θ=45°时，∠ANC的度数为______；
②如图b，当θ≠45°时，①中的结论是否发生变化？说明理由；
（2）如图c，当∠BAC=∠MBN≠90°时，请直接写出∠ANC与∠BAC之间的数量关系，不必证明．
（北师大版）用四块如图①所示的正方形瓷砖拼成一个新的正方形，使拼成的图案是一个轴对称图形．请你在图②、图③、图④中各画一种拼法（要求三种拼法各不相同，且其中至少一个既是轴对称图形，又是中心对称图形）．
如图所示，网格中每个小正方形的边长为1，请你认真观察图（1）中的三个网格中阴影部分构成的图案，解答下列问题：
（1）这三个图案都具有以下共同特征：都是对称图形，都不是对称图形．
（2）请在图（2）中设计出一个面积为4，且具备上述特征的图案，要求所画图案不能与图（1）中所给出的图案相同．
粤公网安备 44130202000953号