四边形 是边长为2的正方形, 是 的中点,连结 ,点 是射线 上一动点(不与点 重合),连结 ,交 于点 .
(1)如图1,当点 是 边的中点时,求证: ;
(2)如图2,当点 与点 重合时,求 的长;
(3)在点 运动的过程中,当线段 为何值时, ?请说明理由.

如图,在矩形 中, , ,点 、 在 边上, 和 交于点 ,若 ,则图中阴影部分的面积为
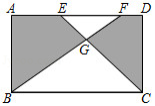
A.25B.30C.35D.40
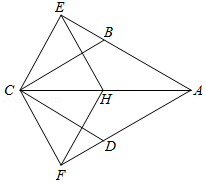
如图,在边长为 的正方形 中,点 , 分别是边 , 的中点,连接 , ,点 , 分别是 , 的中点,连接 ,则 的长度为 .

如图,在 中, ,边 在 轴上,顶点 , 的坐标分别为 和 .将正方形 沿 轴向右平移,当点 落在 边上时,点 的坐标为

A. , B. C. , D.
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.
如图, 为 的直径, 为 上一点, ,垂足为 , 平分 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,平行四边形 的对角线 , 相交于点 , 是 的中点.则 与 的面积的比等于

A. B. C. D.
如图,四边形 是菱形,点 为对角线 的中点,点 在 的延长线上, ,垂足为 ,点 在 的延长线上, ,垂足为 ,
(1)若 ,求证:四边形 是菱形;
(2)若 , 的面积为16,求菱形 的面积.

如图, 为 的直径, 为 上一点, ,垂足为 , 平分 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
如图,平行四边形 的对角线 , 相交于点 , 是 的中点.则 与 的面积的比等于

A. B. C. D.
在矩形 中, , ,点 在对角线 上,圆 的半径为2,如果圆 与矩形 的各边都没有公共点,那么线段 长的取值范围是 .
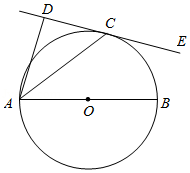
如图,已知 是 的直径,直线 与 相切于点 ,过点 作 交 于点 ,连接 .
(1)求证: 是 的切线.
(2)若 ,直径 ,求线段 的长.

如图,在 中, ,点 为 上一点,以 为直径的 交 于点 ,连接 ,且 平分 .
(1)求证: 是 的切线;
(2)连接 ,若 ,求 .

(1)如图1,将矩形 折叠,使 落在对角线 上,折痕为 ,点 落在点 处,若 ,则 的度数为 .
(2)小明手中有一张矩形纸片 , , .
【画一画】
如图2,点 在这张矩形纸片的边 上,将纸片折叠,使 落在 所在直线上,折痕设为 (点 , 分别在边 , 上),利用直尺和圆规画出折痕 (不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
【算一算】
如图3,点 在这张矩形纸片的边 上,将纸片折叠,使 落在射线 上,折痕为 ,点 , 分别落在点 , 处,若 ,求 的长;
【验一验】
如图4,点 在这张矩形纸片的边 上, ,将纸片折叠,使 落在 所在直线上,折痕为 ,点 , 分别落在点 , 处,小明认为 所在直线恰好经过点 ,他的判断是否正确,请说明理由.
