已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为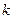 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
①当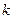 = 1时,是 ;
= 1时,是 ;
②当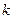 = 2时,是 ;
= 2时,是 ;
③当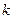 = 3时,是 .
= 3时,是 .
请证明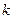 = 2时的结论.
= 2时的结论.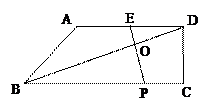

(本题14分)如图11,在△ABC中,∠ACB= ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,
CH⊥BM于H.
(1)试求sin∠MCH的值;
(2)求证:∠ABM=∠CAH;
(3)若D是边AB上的点,且使△AHD为等腰三角形,请直接写出AD的长为________.
如图,在□ABCD中, ,
, .点
.点 由
由 出发沿
出发沿 方向匀速运动,速度为
方向匀速运动,速度为 ;同时,线段
;同时,线段 由
由 出发沿
出发沿 方向匀速运动,速度为
方向匀速运动,速度为 ,交
,交 于
于 ,连接
,连接 、
、 .若设运动时间为
.若设运动时间为 (s)(
(s)( ).解答下列问题:
).解答下列问题:
(1)当 为何值时,
为何值时, ∥
∥ ?并求出此时
?并求出此时 的长;
的长;
(2)试判断△ 的形状,并请说明理由.
的形状,并请说明理由.
(3)当 时,
时,
(ⅰ)在上述运动过程中,五边形 的面积 ▲ (填序号)
的面积 ▲ (填序号)
①变大 ②变小 ③先变大,后变小 
 ④不变
④不变
(ⅱ)设 的面积为
的面积为 ,求出
,求出 与
与 之间的函数关系式及
之间的函数关系式及 的取值范围.
的取值范围.
(8分) (1)学习《测量建筑物的高度》后,小明带着卷尺、标 杆,利用太
杆,利用太
阳光去测量旗杆的高度.
参考示意图1,他的测量方案如下:
第一步,测量数据.测出CD=1.6米,CF=1.2米, AE=9米.
第二步,计算.
请你依据小明的测量方案计算出旗杆的高度.
(2) 如图2,校园内旗杆周围有护栏,下面有底座.现在有卷尺、标杆、平面镜、测角仪等工具,请你选择 出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
要求:在备 用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
你选择出的必须工具是 ;
需要测量的数据是 .
已知,边长为5的正方形ABCO在如图所示的直角坐标系中,点
M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.
(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
如图,点P为等边△ABC外接圆劣弧BC上一点.
(1)求∠BPC的度数;
(2)求证:PA=PB+PC;
(3)设PA,BC交于点M,若AB=4,PC=2,求CM的长度.
如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.


如图,在边长为8的正方形ABCD
中,点O为AD上一动点(4<OA<8),以O为圆心 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1) 求证:△ODM∽△MCN;
(2) 设DM=x,求OA的长(用含x的代数式表示);
(3) 在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
(本题满分7分)如图5,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点
P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得
到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1)如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 ▲ 关
系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP="β" . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△
AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面积为
S,求S关于x的函数关系式.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
(本小题满分12分)图形既关于点O中心对称,又关于直线AC,BD对称,AC=10,
BD=6,已知点E,M是线段AB上的动点(不与端点重合),点O到EF,MN的距离分别
为 ,
,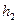 ,△OEF与△OGH组成的图形称为蝶形。
,△OEF与△OGH组成的图形称为蝶形。
(1)求蝶形面积S的最大值;
(2)当以EH为直径的圆与以MQ为直径的圆重合时,求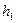 与
与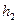 满足的关系式,并求
满足的关系式,并求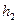 的取值范围。
的取值范围。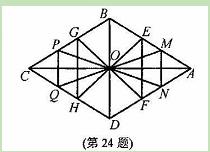
如图所示,P是⊙O外一点,PA是⊙O的切线,A是切点,B是⊙O 上一点,且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q.
(1)求证:PB是⊙O的切线;
(2)求证:AQ•PQ=OQ•BQ;
(3)设∠AOQ=α,若cosα= ,OQ=15,求AB的长.
,OQ=15,求AB的长.
(满分8分)如图,BD是⊙O的直径, A、C是⊙O上的两点,且AB=AC,
AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.
在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数 (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F.
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.