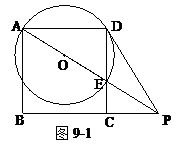
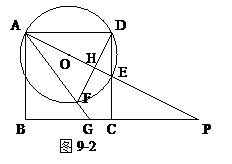如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.
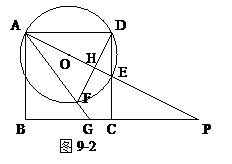
相关知识点
推荐套卷
如图9-1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长 线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE = x,PC = y.
(1)求y与x之间的函数关系式;
(2)若PD是⊙O的切线,求x的值.
(3)过点D作DF⊥AE,垂足为H,交⊙O于点F,直线AF交BC于点G(如图9-2).若x=2,则sin∠BAG的值是_________.