2011届南京市雨花台中考数学一模试卷
如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O—C—D—O
路线作匀速运动,设运动时间为x(秒),∠APB=y(度),右图函数图象表示y与x之间函数
关系,则点M的横坐标应为( ▲ )
| A.2 | B. |
C. |
D. +2 +2 |
某农户2008年的年收入为5万元,由于党的惠农政策的落实,2010年年收入增
加到7.2万元,则平均每年的增长率是 ▲____.
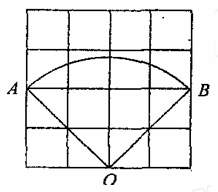
如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方
形.O、A、B分别是小正方形的顶点,则扇形OAB的弧长等于 ▲ .(结果保留根
号及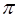 ).
).
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图
形,甲、乙这10次射击成绩的方差 ,
, 之间的大小关系是 ▲ .
之间的大小关系是 ▲ .
(6分 )某市为了提高学生的安全防范意识和能力,每年在全市中小学学生中举
)某市为了提高学生的安全防范意识和能力,每年在全市中小学学生中举
行安全知识竞赛,为了了解今年全市七年级同学的竞赛成绩情况,小强随机调查了一些七年
级同学的竞赛成绩,根据收集到的数据绘制了参与调查学生成绩的频数分布直方图和其中合
格学生成绩的扇形统计图如下:
根据统计图提供的信息,解答以下问题:
(1)小强本次共调查了多少名七年级同学的成绩?被调查的学生中成绩合格的频率是多少?
(2)该市若有10000名七年级学生,请你根据小强的调查统计结果估计全市七年级学生中有多少名学生竞赛成绩合格?对此你有何看法?
(3)填写下表:
| 成绩 |
不合格 |
合格但不优秀 |
合格且优秀 |
| 频率 |
0.2 |
▲ |
▲ |
如图,在一滑梯侧面示意图中,BD∥AF,BC⊥AF于点C,DE⊥AF于
点E.BC=1.8m,BD=0.5m,∠A=45º,∠F=29º.
(1)求滑道DF的长(精确到0.1m);
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m).
(参考数据:sin29º≈0.48,cos29º≈0.87,tan29º≈0.55)
写出下列命题的已知、求证,并完成证明过程.
命 题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边
题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边 ”) .
”) .
已知:如图,___ _▲_ ____.
求证:___ _▲_ ____.
证明:
小明同学看到路边上有人设摊玩“有奖掷币”游戏,规则是:交2元钱
可以玩一次掷硬币游戏,每次同时掷两枚硬币,如果出现两枚硬币正面朝上,奖金5元;如
果是其它情况,则没有奖金(每枚硬币落地只有正面朝上和反面朝上两种情况).小明拿不
定主意究竟是玩还是不玩,请同学们帮帮忙!
(1)求出中奖的概率;
(2)如果有100人,每人玩一次这种游戏,大约有 ▲ 人中奖,奖金共约是 ▲ 元;设摊者约获利 ▲ 元;
(3)通过以上“有奖”游戏,你从中可得到什么启示?
如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半
径的⊙A交x轴于点B、C.解答下列问题: (1)将⊙A向左平移____▲_____个单位长度与y轴首次相切,得到⊙A1.此时点A1的坐标为____▲_____,阴影部分的面积S=____▲_____;
(1)将⊙A向左平移____▲_____个单位长度与y轴首次相切,得到⊙A1.此时点A1的坐标为____▲_____,阴影部分的面积S=____▲_____;
(2)求BC的长.
函数 的图象如图所示.
的图象如图所示.
(1) (
( )是第一象限内图象上的点,且
)是第一象限内图象上的点,且 都是整数.求出所有的点
都是整数.求出所有的点 ;
;
(2)若P(m,y1),Q(-3,y2)是函数 图象上的两点,且y1> y2,求实数m的取值范围.
图象上的两点,且y1> y2,求实数m的取值范围.
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸
货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图
所示.解答下列问题:
(1)这辆汽 车的往、返速度是否相同?请说明理由;
车的往、返速度是否相同?请说明理由;
(2)求这辆汽车从甲地出发4h时与甲地的距离.
在平面上有且只有4个点,这4个点中有一个独特的性质:连结每两点可得到6条线段,这6条线段有且只有两种长度.我们把这四个点称作准等距点.例如正方形ABCD的四个顶点(如图1),有AB=BC=CD=DA,AC=BD.其实满足这样性质的图形有很多,如图2中A、B、C、O四个点,满足AB=BC=CA,OA=OB=OC;如图3中A、B、C、O四个点,满足OA=OB=OC=BC,AB=AC.

(1)如图,若等腰梯形ABCD的四个顶点是准等距点,且AD∥BC.
①写出相等的线段(不再添加字母);
②求∠BCD的度数.
(2)请再画出一个四边形,使它的四个顶点为准等距点,并写出相等的线段.
某电子科技公司开发一种新产品.产品投产上市一年来,公司经历了由
初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司
前12个月累积获得的利润y(万元)与销售时间第x(月)之间的函数关系(即前x个月的
利润总和y与x之间的关系)对应的点都在如图所示的图 象上.该图象是某二次函数
象上.该图象是某二次函数
y=a(x-h)2+k图象的一部分,点A为抛物线的顶点,且点A,B,C的横坐标分别为4,10,
12,点A,B的纵 坐标分别为-16,20.
坐标分别为-16,20.
(1)求前12个月该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)分别求出前9个月公司累积获得的利润和10月份一个月内所获得的利润;
(3)在前12个月中,哪个月该公司一个月内所获得的利润最多?最多利润是多少万元?
已知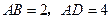 ,
,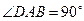 ,
,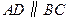 (如图).
(如图).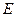 是射线
是射线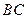 上的动点(点
上的动点(点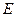 与点
与点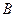 不重合),
不重合),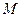 是线段
是线段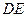 的中点.
的中点.
(1)设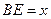 ,
,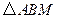 的面积为
的面积为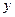 ,求
,求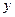 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)如果以线段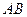 为直径的圆与以线段
为直径的圆与以线段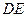 为
为 直径的圆外切,求线段
直径的圆外切,求线段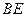 的长;
的长;
(3)连结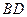 ,交线段
,交线段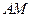 于点
于点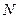 ,如果以
,如果以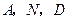 为顶点的三角形与
为顶点的三角形与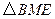 相似,求线段
相似,求线段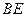 的长.
的长.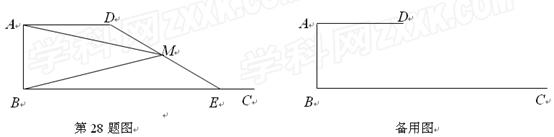
检测4袋食盐,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,下列检测结果中,最接近标准质量的是( ▲ )
| A.+0.7 | B.+2.1 | C.-0.8 | D.-3.2 |
小明和爸爸妈妈三人玩跷跷板,爸爸坐在跷跷板的一端,小明和妈妈一同坐在跷跷板的另一端,他们都不用力时;爸爸那端着地,已知爸爸的体重为70千克,妈妈的体重为50千克,那么小明的体重可能是( ▲ )
|
| A.18千克 | B.22千克 | C.28千克 | D.30千克 |
二次函数 的图象如图所示,若点A(1,y1)、B(2,y2)是
的图象如图所示,若点A(1,y1)、B(2,y2)是
它图象上的两点,则y1与y2的大小关系是( ▲ )
A. |
B. |
C. |
D.不能确定 |
某班6名同学在一次“1分钟仰卧起坐”测试中,成绩分别为(单位:次):39,
45,42,37,41,39.这组数据的众数、中位数分别是
| A.42,37 | B.41,42 | C.39,41 | D.39,40 |
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A
的纵坐标是1,则点B的坐标是
| A.(3,1) | B. |
C. |
D.(1,3) |
如图,矩形ABCD中, ,
, ,点P从点B出发,沿
,点P从点B出发,沿 向终
向终
点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数
关系的图象是
A B C D
我国因环境污染造成的巨大经济损失每年高达680 000 000元,680 000 000用科
学记数法表示为 ▲ .
如图,三角板 中,
中, ,
, ,
, .三角板绕直角
.三角板绕直角
顶点 逆时针旋转,当点
逆时针旋转,当点 的对应点
的对应点 落在
落在 边的起始位置上时即停止转动,则点
边的起始位置上时即停止转动,则点 转
转
过的路径长为 ▲ .
(6分)下面的图①、图②分别是一所学校调查部分学生是否知道母亲生日情况的
扇形统计图和条形统计图:

根据上图信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若这所学校共有2700名学生,你估计该校有多少名学生知道母亲的生日?
.(6分)一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm(点A 、B、C在同一直线上),点A到地面的距离AD=8cm,旅行箱与水平面AE成50°角,求拉杆伸长到最大时,把手处C到地面的距离(精确到1cm).(参考数据:sin50°= 0.77,cos50°= 0.64,tan50°= 1.19.)
、B、C在同一直线上),点A到地面的距离AD=8cm,旅行箱与水平面AE成50°角,求拉杆伸长到最大时,把手处C到地面的距离(精确到1cm).(参考数据:sin50°= 0.77,cos50°= 0.64,tan50°= 1.19.)
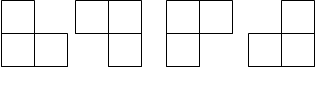
如图,在3×3的正方形网格中,每个网格都有三个小正方形被涂黑.
(1)在图①中将一个空白部分的小正方形涂黑,使其余空白部分是轴对称图形但不是中心对称图形.
(2)在图②中将两个空白部分的小正方形涂黑,使其余空白部分是中心对称图形但不是轴对称图形.
( 8分)某校组织学生到外地进行综合实践活动,共有680名学生参加,并携带300件行李.学校计划租用甲、乙两种型号的汽车共20辆.经了 解,甲种汽车每辆最多能载40人和10件行李,乙种汽车
解,甲种汽车每辆最多能载40人和10件行李,乙种汽车 每辆最多能载30人和20件行李.
每辆最多能载30人和20件行李.
⑴如何安排甲、乙两种汽车可一次性地将学生和行李全部运走?有哪几种方案?
⑵如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案
如图,有两个可以自由转动的均匀转盘 、
、 ,转盘
,转盘 上一条直径与一条半径垂直,转盘
上一条直径与一条半径垂直,转盘 被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
①分别转动转盘 与
与
 ;
;
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止);
③如果和为0,则小明获胜;否则小刚获胜.
(1)用列表法(或树状图)求小明获胜的概率;
(2)你认为这个游戏对双方公平吗?如果你认为不公平,请适当改动规则使游戏对双方公平.
.(8分)如图,四边形 是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。
是平行四边形,以AB为直径的⊙O经过点D,点E是⊙O上一点,且∠AED=45°。
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为 ,
, ,求∠ADE的正弦值.
,求∠ADE的正弦值.
甲、乙两车同时从 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向 地行驶.甲车先到达
地行驶.甲车先到达 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离 (千米)与乙车行驶时间
(千米)与乙车行驶时间 (小时)之间的
(小时)之间的 函数图象.
函数图象.
(1)两车行驶3小时后,两车相距 ▲ 千米;
(2)请在图中的( )内填上正确的值,并直接写出甲车从 到
到 的行驶速度;
的行驶速度;
(3)求从甲车返回到与乙车相遇过程中 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值
的取值
范围.
(4)求出甲车返回时的行驶速度及 、
、 两地之间的距离.
两地之间的距离.
如图,△ABC中,点O在边AB上,过点O作BC的平行线交∠ABC
的平分线于点D,过点B作BE⊥BD,交直线OD于点E。
(1)求证:OE=OD ;
(2)当点O在什么位置时,四边形BDAE是矩形 ?说明理由;
?说明理由;
(3)在满足(2)的条件下,还需△ABC满足什么条件时,四边形BDAE是正方形?写出你确定的条件,并画出图形,不必证明。
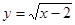 中,自变量
中,自变量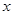 的取值范围是 ▲ .
的取值范围是 ▲ .
 ▲ .
▲ .


 .
. ,其中
,其中 .
.


 的图象位于第二、四象限,则
的图象位于第二、四象限,则 的取值可以是
的取值可以是 中自变量的取值范围是 ▲ .
中自变量的取值范围是 ▲ . 的解是 ▲ .
的解是 ▲ . 按如图折叠,若
按如图折叠,若 点坐标为(4,
点坐标为(4, ,则
,则 的坐标为 ▲ .
的坐标为 ▲ . 
 ,若
,若 ,则
,则 ▲ 度.
▲ 度.
 ,则原二次函数的表达式为 ▲ .
,则原二次函数的表达式为 ▲ . 的圆形纸片折叠后,圆弧恰好经过圆心
的圆形纸片折叠后,圆弧恰好经过圆心 ,则折痕
,则折痕 的
的 .
.


 ,其中
,其中
 ,
, .点
.点 由
由 出发沿
出发沿 方向匀速运动,速度为
方向匀速运动,速度为 ;同时,线段
;同时,线段 由
由 出发沿
出发沿 方向匀速运动,速度为
方向匀速运动,速度为 于
于 ,连接
,连接 、
、 .若设运动时间为
.若设运动时间为 (s)(
(s)( ).解答下列问题:
).解答下列问题: ?并求出此时
?并求出此时 的形状,并请说明理由.
的形状,并请说明理由. 时,
时, 的面积 ▲ (填序号)
的面积 ▲ (填序号)
 ④不变
④不变 的面积为
的面积为 ,求出
,求出 之间的函数关系式及
之间的函数关系式及 的取值范围.
的取值范围.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号