如图,有两个可以自由转动的均匀转盘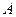 、
、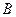 ,转盘
,转盘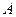 上一条直径与一条半径垂直,转盘
上一条直径与一条半径垂直,转盘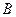 被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
被分成相等的3份,并在每份内均标有数字.小明和小刚用这两个转盘做游戏,游戏规则如下:
①分别转动转盘 与
与
 ;
;
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止);
③如果和为0,则小明获胜;否则小刚获胜.
(1)用列表法(或树状图)求小明获胜的概率;
(2)你认为这个游戏对双方公平吗?如果你认为不公平,请适当改动规则使游戏对双方公平.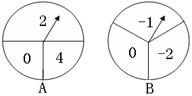
相关知识点
推荐套卷
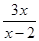 -
-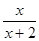 )·
)·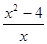 ,再选一个你喜欢的x的值代入求值。
,再选一个你喜欢的x的值代入求值。 ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2. ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
 ,sin∠BCP=
,sin∠BCP= ,求点B到AC的距离.
,求点B到AC的距离.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号