如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,tan∠AOB= ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
(1)求抛物线的解析式.
(2)在第三象限内,抛物线上的点P在什么位置时,△PBB1的面积最大?求出这时点P的坐标.
(3)在第三象限内,抛物线上是否存在点Q,使点Q到线段BB1的距离为 ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
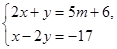 的解x,y都是正数,求m的取值范围.
的解x,y都是正数,求m的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号