在一个不透明的盒子中,共有“一白三黑” 个围棋子,它们除了颜色之外没有其它区别.
个围棋子,它们除了颜色之外没有其它区别.
(1)随机地从盒中提出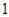 子,则提出白子的概率是多少?
子,则提出白子的概率是多少?
(2)随机地从盒中提出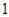 子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.
子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.
相关知识点
推荐套卷
在一个不透明的盒子中,共有“一白三黑” 个围棋子,它们除了颜色之外没有其它区别.
个围棋子,它们除了颜色之外没有其它区别.
(1)随机地从盒中提出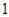 子,则提出白子的概率是多少?
子,则提出白子的概率是多少?
(2)随机地从盒中提出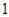 子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.
子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.