如图，在一滑梯侧面示意图中，BD∥AF，BC⊥AF于点C，DE⊥AF于
点E．BC＝1.8m，BD＝0.5m，∠A＝45º，∠F＝29º．
(1)求滑道DF的长(精确到0.1m)；
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m)．
(参考数据：sin29º≈0.48，cos29º≈0.87，tan29º≈0.55)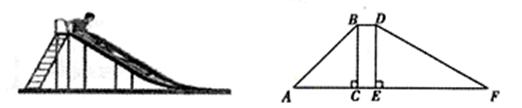
相关知识点
推荐套卷
如图，在一滑梯侧面示意图中，BD∥AF，BC⊥AF于点C，DE⊥AF于
点E．BC＝1.8m，BD＝0.5m，∠A＝45º，∠F＝29º．
(1)求滑道DF的长(精确到0.1m)；
(2)求踏梯AB底端A与滑道DF底端F的距离AF(精确到0.1m)．
(参考数据：sin29º≈0.48，cos29º≈0.87，tan29º≈0.55)
粤公网安备 44130202000953号