如图①,△ABC中,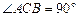 ,∠ABC=
,∠ABC=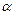 ,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是
,将△ABC绕点A顺时针旋转得到△AB ¢C ¢,设旋转的角度是 .
.
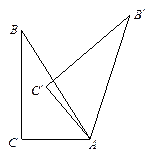

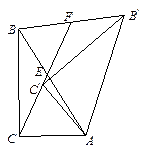
(1)如图②,当 =" " °(用含
=" " °(用含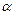 的代数式表示)时,点B ¢恰好落在CA的延长线上;
的代数式表示)时,点B ¢恰好落在CA的延长线上;
(2)如图③,连结BB ¢、CC ¢, CC ¢的延长线交斜边AB于点E,交BB ¢于点F.请写出图中两对相似三角形 ,
(不含全等三角形),并选一对证明.
含30°角的直角三角板ABC中,∠A=30°.将其绕直角顶点C顺时针旋转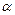 角(
角(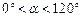 且
且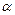 ≠ 90°),得到Rt△
≠ 90°),得到Rt△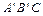 ,
,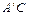 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥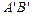 交
交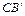 边于点E,连接BE.
边于点E,连接BE.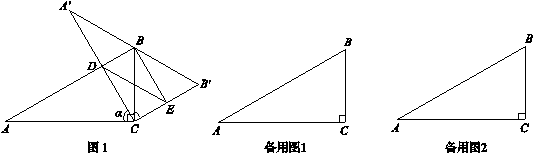
(1)如图1,当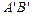 边经过点B时,
边经过点B时,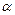 = °;
= °;
(2)在三角板旋转的过程中,若∠CBD的度数是∠CBE度数的m倍,猜想m的值并证明你的结论;
(3) 设 BC=1,AD=x,△BDE的面积为S,以点E为圆心,EB为半径作⊙E,当S=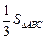
时,求AD的长,并判断此时直线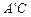 与⊙E的位置关系.
与⊙E的位置关系.
已知:如图,在△ABC中,AB="AC=" 5,BC= 8,D,E分别为BC,AB边上一点,∠ADE=∠C.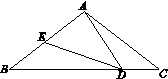
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.
(1)如图1,若 和
和 分别是以
分别是以 与
与 为顶角的等腰直角三角形,且两三角形旋转到使点
为顶角的等腰直角三角形,且两三角形旋转到使点 、
、 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系;
(2)若 和
和 为含有
为含有 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 与线段
与线段 的关系,并说明理由;
的关系,并说明理由;
(3)若 和
和 为如图3的两个三角形,且
为如图3的两个三角形,且 =
= ,
, ,在绕点
,在绕点 旋转的过程中,直线
旋转的过程中,直线 与
与 夹角的度数是否改变?若不改变,直接用含
夹角的度数是否改变?若不改变,直接用含 、
、 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由.
用棋子摆出下列一组图形:
(1)、填写下表:
| 图形编号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 图中棋子数 |
5 |
8 |
11 |
14 |
|
|
(2)、照这样的方式摆下去,写出摆第 个图形所需棋子的枚数;
个图形所需棋子的枚数;
(3)、其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形
学习《图形的相似》后,我们可以探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件.
(1)“对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,两个直角三角形全等”,类似地,你可以得到“满足_____,或_____,两个直角三角形相似”;
(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到满足_____两个直角三角形相似”.请结合下列所给图形,写出已知,并完成说理过程.
已知:如图,_____.试说明Rt△ABC∽Rt△A/B/C/.
如图9,在△ABC中,D是BC的中点, DE⊥AB于E,DF⊥AC于点F,且BE=CF,求证AD⊥BC。
DE⊥AB于E,DF⊥AC于点F,且BE=CF,求证AD⊥BC。
如图8,已知点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF,求证:△ABC≌△DEF。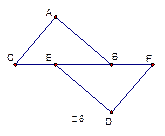
如图10,已知 ,
, ,
, 与
与 相交于点
相交于点 ,连接
,连接


(1)图中还有几对全等三角形,请你一一列举.
(2)求证: