北京市昌平区初三上学期期末考试数学卷
教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. |
B.1 | C. |
D.2 |
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知 ,其中
,其中 为锐角,试求sad
为锐角,试求sad 的值.
的值.
已知二次函数 .
.
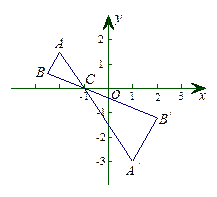
(1)求此二次函数图像与x轴交点A、B(A在B的左边)的坐标;
(2)若此二次函数图像与y轴交于点C、且△AOC∽△COB(字母依次对应).
①求a的值;
②求此时函数图像上关于原点中心对称的两个点的坐标.
如图,在梯形ABCD中,AB‖CD,∠A= ,AB=3,CD=6,BE⊥BC交直线AD于点E.
,AB=3,CD=6,BE⊥BC交直线AD于点E. 
(1)当点E与D恰好重合时,求AD的长;
(2)当点E在边AD上时(E不与A、D重合),设AD=x,ED=y,试求y关于x的函数关系式,并写出定义域;
(3)问:是否可能使△ABE、△CDE与△BCE都相似?若能,请求出此时AD的长;若不能,请说明理由.
下列判断错误的是( )
| A.若a = b,则ac-3 = bc-3 | B.若a = b,则 |
| C.若x = 2,则x2 =" 2x" | D.若ax = bx,则a = b |
一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件作服装仍可获利15元,则这种服装每件的成本是( )
| A.120元 | B.125元 | C.135元 | D.140元 |
下列变形符合等式性质的是( )
| A.如果2x-3=7,那么2x=7-3 . | B.如果3x-2=x+1,那么3x-x=1-2. |
| C.如果-2x=5,那么x="5+2" . | D.如果-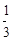 x=1,那么x=-3. x=1,那么x=-3. |
观察下列算式:71=7,72=49,73=343,74=2401,…根据上述算式中的规律,你认为72010的个位数字是( )
| A.7 | B.9 | C.3 | D.1 |
一家 商店将某种商品
商店将某种商品 按成本价提高40%后标价,元旦期间,欲打八折销售,以答谢新老顾客对
按成本价提高40%后标价,元旦期间,欲打八折销售,以答谢新老顾客对 本商厦的光顾,售价为224元,这件商品的成本价是多少元?
本商厦的光顾,售价为224元,这件商品的成本价是多少元?
下列事件中,必然事件是
| A.任意掷一枚均匀的硬币,正面朝上 |
| B.打开电视正在播放甲型H1N1流感的相关知识 |
| C.某射击运动员射击一次,命中靶心 |
| D.在只装有5个红球的袋中摸出1球,是红球 |
图是一个表示“众志成城,奉献爱心”的图标,图标中两圆的位置关系是
| A.外离 | B.内含 | C.外切 | D.内切 |
如图,扇形纸片的圆心角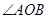 为
为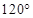 ,弦AB的长为
,弦AB的长为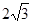 cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为
cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为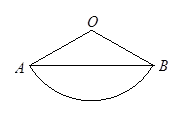
A.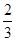 cm cm |
B.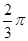 cm cm |
C.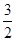 cm cm |
D.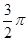 cm cm |
如图,已知点 ,
, ,
, ,在
,在 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在 轴上,另一个顶点在
轴上,另一个顶点在 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个 ,第2个
,第2个 ,第3个
,第3个 ,…,则第1个等边三角形的边长等于 , 第
,…,则第1个等边三角形的边长等于 , 第 (
( ,且
,且 为整数)个等边三角形的边长等于
为整数)个等边三角形的边长等于 
如图,在正方形网格中,每个小正方形的边长都为1,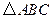 的顶点都在格点(小正方形的顶点)上,将
的顶点都在格点(小正方形的顶点)上,将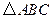 绕点
绕点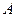 按逆时针方向旋转
按逆时针方向旋转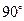 得到
得到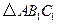 .
.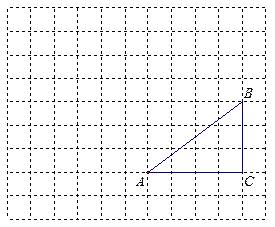
(1)在正方形网格中,画出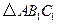 ;
;
(2)直接写出旋转过程中动点 所经过的路径长.
所经过的路径长.
已知二次函数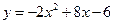 .
.
(1)求二次函数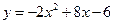 的图象与两个坐标轴的交点坐标;
的图象与两个坐标轴的交点坐标;
(2)在坐标平面上,横坐标与纵坐标都是整数的点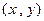 称为整点. 直接写出二次函数
称为整点. 直接写出二次函数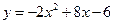 的图象与
的图象与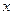 轴所围成的封闭图形内部及边界上的整点的个数.
轴所围成的封闭图形内部及边界上的整点的个数.
如图,小明在十月一日到公园放风筝,风筝飞到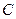 处时的线长为20米,此时小明正好站在A处,并测得
处时的线长为20米,此时小明正好站在A处,并测得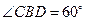 ,牵引底端
,牵引底端 离地面1.5米,求此时风筝离地面的高度.
离地面1.5米,求此时风筝离地面的高度.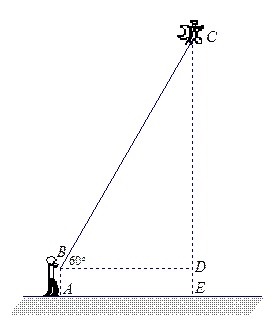
下图是由转盘和指针组成的装置 、
、 ,两个转盘分别被分成三个面积相等的扇形. 装置
,两个转盘分别被分成三个面积相等的扇形. 装置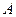 上的数字分别是1,6,8,装置
上的数字分别是1,6,8,装置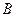 上的数字分别是4,5,7. 这两个装置除了表面数字不同外,其他构造完全相同. 现在你和另外一个同学分别同时用力转动装置
上的数字分别是4,5,7. 这两个装置除了表面数字不同外,其他构造完全相同. 现在你和另外一个同学分别同时用力转动装置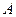 、
、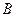 中的指针,如果我们规定指针停留在较大数字的一方获胜(若指针恰好停留在分界线上,则重新转动
中的指针,如果我们规定指针停留在较大数字的一方获胜(若指针恰好停留在分界线上,则重新转动 一次,直到指针停留在某一数字为止),那么你选择的装置是 ,请说明理由.
一次,直到指针停留在某一数字为止),那么你选择的装置是 ,请说明理由.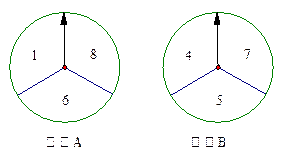
心理学家经过调查发现,某班级的学生对概念的接受能力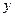 与提出概念所用的时间
与提出概念所用的时间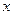 (单位:分)之间满足函数关系:
(单位:分)之间满足函数关系: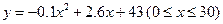 .其中,
.其中,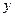 值越大,表示接受能力越强.
值越大,表示接受能力越强.
(1)第10分钟时,学生的接受能力是多少?
(2)第几分时,学生的接受能力最强?
(3)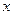 在什么范围内,学生的接受能力逐步增强?
在什么范围内,学生的接受能力逐步增强?
如图,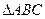 中,
中,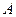 、
、 两点在
两点在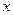 轴的上方,点
轴的上方,点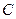 的坐标是(-1,0).以点
的坐标是(-1,0).以点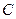 为位似中心,在
为位似中心,在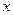 轴的下方作
轴的下方作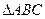 的位似图形
的位似图形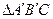 ,并把
,并把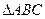 的边长放大到原来的2倍.设点
的边长放大到原来的2倍.设点 的对应点
的对应点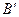 的横坐标是2,求点
的横坐标是2,求点 的横坐标
的横坐标
(1)如图1,请你类比直线和一个圆的三种位置关系,在图1的①、②、③中,分别各画出一条直线,使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交,并在图1的④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系;
(2)如图2,点 、
、 在直线MN上,AB=11厘米,
在直线MN上,AB=11厘米, 、
、 的半径均为1厘米.
的半径均为1厘米. 以每秒2厘米的速度自左向右运动,与此同时,
以每秒2厘米的速度自左向右运动,与此同时, 的半径
的半径 也不断增大,其半径
也不断增大,其半径 (厘米)与时间t(秒)之间的关系式为
(厘米)与时间t(秒)之间的关系式为  .请直接写出点
.请直接写出点 出发后多少秒两圆内切?
出发后多少秒两圆内切?
如图,在平面直角坐标系 中,二次函数
中,二次函数 的图象经过点
的图象经过点 ,顶点为
,顶点为 .
.
(1)求这个二次函数的解析式;
(2)若点 的坐标为
的坐标为 ,连接
,连接 ,过点
,过点 作
作 ,垂足为点
,垂足为点 .当点
.当点 在直线
在直线 上,且满足
上,且满足 时,求点
时,求点 的坐标.
的坐标.
 C:-
C:-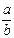
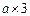
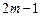 个
个
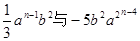 是同类项,则n=( )
是同类项,则n=( )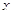 = 1;
= 1; = 0
= 0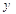 + 1
+ 1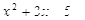 的值为7,则
的值为7,则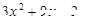 的值为( )
的值为( )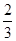 πa2的系数是_______
πa2的系数是_______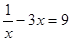 , ③
, ③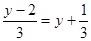 , ④
, ④ ,是一元一次方程的有 。(填题号)
,是一元一次方程的有 。(填题号)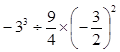
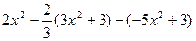 ,其中
,其中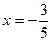
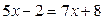
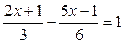
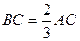 ,D为BC的中点,求BC、AD的长
,D为BC的中点,求BC、AD的长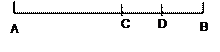




 有意义,
有意义, 必须满足的条件是
必须满足的条件是








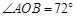 ,则
,则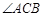 的度数是
的度数是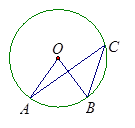
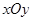 中,
中,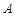 点坐标为
点坐标为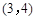 ,将
,将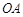 绕原点
绕原点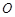 顺时针旋转
顺时针旋转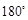 得到
得到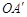 ,则点
,则点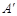 的坐标是
的坐标是 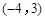
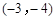
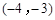
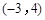
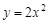 向上平移5个单位,所得抛物线的解析式为
向上平移5个单位,所得抛物线的解析式为 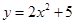
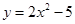

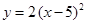
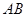 的坡度
的坡度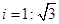 ,则坡角
,则坡角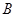 的度数为
的度数为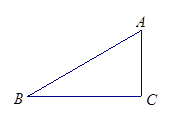
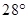
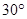
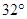
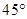
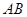 、
、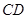 是同心圆中半径最大的圆的直径,且
是同心圆中半径最大的圆的直径,且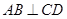 于点
于点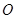 ,若
,若 ,则图中阴影部分的面积等于
,则图中阴影部分的面积等于 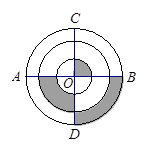
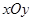 中,点
中,点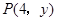 在第一象限内,且
在第一象限内,且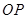 与
与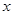 轴正半轴的夹角为
轴正半轴的夹角为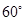 ,则
,则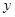 的值是
的值是 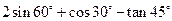
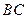 是
是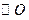 的直径,
的直径,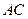 切
切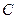 .若sin
.若sin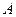 =
=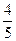 ,
,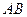 =15,求△
=15,求△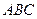 的周长
的周长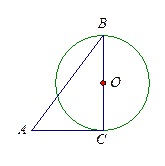
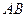 是⊙O的直径,
是⊙O的直径,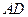 是弦,
是弦,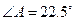 ,延长
,延长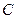 ,使得
,使得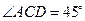 .
.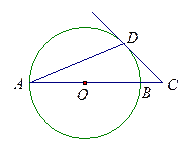
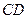 是⊙O的切线;
是⊙O的切线;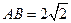 ,求
,求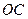 的长
的长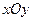 中,
中,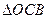 的外接圆与
的外接圆与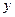 轴交于点
轴交于点 ,
,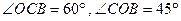 ,
, 求
求 的长.
的长.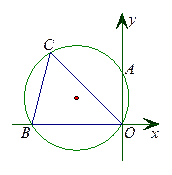
 和
和 是绕点
是绕点 旋转的两个相似三角形,其中
旋转的两个相似三角形,其中 与
与 、
、 与
与 为对应角.
为对应角.
 、
、 在同一条直线上的位置时,请直接写出线段
在同一条直线上的位置时,请直接写出线段 与线段
与线段 的关系;
的关系; 角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段
角的直角三角形,且两个三角形旋转到如图2的位置时,试确定线段 =
= ,
, ,在绕点
,在绕点 的式子表示夹角的度数;若改变,请说明理由.
的式子表示夹角的度数;若改变,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号