（1）如图1，请你类比直线和一个圆的三种位置关系，在图1的①、②、③中，分别各画出一条直线，使它与两个圆都相离、与两个圆都相切、与一个圆相离且与另一个圆相交，并在图1的④中也画上一条直线，使它与两个圆具有不同于前面3种情况的位置关系；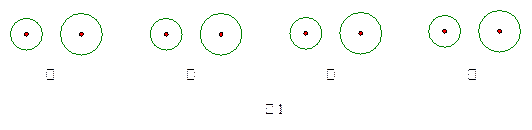
（2）如图2，点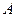
、
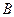在直线MN上，AB＝11厘米，
、
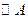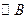的半径均为1厘米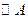．以每秒2厘米的速度自左向右运动，与此同时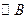，的半径
也不断增大，其半径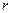
（厘米）与时间t（秒）之间的关系式为 
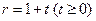．请直接写出点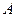出发后多少秒两圆内切？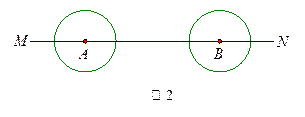
相关试题
有4张看上去无差别的卡片，上面分别写有数 ，2，5，8．
（1）随机抽取一张卡片，则抽取到的数是偶数的概率为 ；
（2）随机抽取一张卡片后，放回并混在一起，再随机抽取一张，请用画树状图或列表法，求抽取出的两数之差的绝对值大于3的概率．
如图，直线 交 轴于点 ，交 轴于点 ，抛物线 经过点 ，点 ，且交 轴于另一点 ．
（1）直接写出点 ，点 ，点 的坐标及拋物线的解析式；
（2）在直线 上方的抛物线上有一点 ，求四边形 面积的最大值及此时点 的坐标；
（3）将线段 绕 轴上的动点 顺时针旋转 得到线段 ，若线段 与抛物线只有一个公共点，请结合函数图象，求 的取值范围．
相关知识点
推荐套卷
粤公网安备 44130202000953号