北京市西城区初三第一学期期末数学卷
在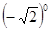
 ,
,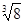 , 0,
, 0, 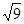 ,
,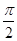 , -0.333…,
, -0.333…,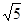 , 3.1415, 2.010101…(相邻两个1之间有1个0)中,无理数有( )
, 3.1415, 2.010101…(相邻两个1之间有1个0)中,无理数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A ′B′C′,则补充的这个条件是:( )
′B′C′,则补充的这个条件是:( )
| A.BC=B′C′ | B.∠A=∠A′ | C.AC=A′C′ | D.∠C=∠C′ |
若正比例函数y=(1-2m)x的图象经过点A(x1 ,y1)和点B(x2 ,y2),当x1 < x 2时,y1>y2,则m的取值范围是( )
2时,y1>y2,则m的取值范围是( )
| A.m<0 | B.m>0 | C. |
D. |
如图,已知A(1,-3),B(-2,-2),C(2,0),
(1)将△ABC向右平移,使B点落在y轴上,画出平移后的△A1B1C1
(2)画出△A1B1C1关于直线y=1对称的△A2B2C2
(3)求S△ABC
如图,AB为⊙O的直径,点C在⊙O上,若∠C=15°,则∠BOC =( ).
| A.60° | B.45° | C.30° | D.15° |
如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则 tan∠ACB的值为( ).
| A.1 | B. |
C. |
D. |
如图,将△ABC的三边分别扩大一倍得到△ (顶点均在格点上),若它们是以P点为位似中心的位似图形,则P点的坐标是( ).
(顶点均在格点上),若它们是以P点为位似中心的位似图形,则P点的坐标是( ).
A. |
B. |
C. |
D. |
某商店购进一种商品,单价为30元.试销中发现这种商品每天的销售量P(件)与每件的销售价x(元)满足关系: .若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).
.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( ).
A. |
B. |
C. |
D. |
如图,△OAB中,OA=OB,∠A=30°,⊙O与AB相切,切点为E,并分别交OA,OB于C,D两点,连接CD.若CD等于 ,则扇形OCED的面积等于( ).
,则扇形OCED的面积等于( ).
A. π B.
π B. π C.
π C. π D.
π D. π
π
如图,OA=4,线段OA的中点为B,点P在以O为圆心,OB为半径的圆上运动,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于( ).
A. |
B. |
C. |
D. |
如图,在△ABC中,DE∥AB分别交AC,BC于点D,E,若AD=2,CD=3,则△CDE与△CAB的周长比为 
如图,平面直角坐标系xOy中,点A ,以OA为半径作⊙O,若点P,B都在⊙O上,且四边形AOPB为菱形,则点P的坐标为
,以OA为半径作⊙O,若点P,B都在⊙O上,且四边形AOPB为菱形,则点P的坐标为 
抛物线 (a ≠ 0)满足条件:
(a ≠ 0)满足条件:
(1) ;
;
(2) ;
;
(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:
① ;②
;② ;③
;③ ;④
;④ ,其中所有正确结论的序号是
,其中所有正确结论的序号是
已知:如图,在Rt△ABC中,∠C=90°,∠ABC=60°,AC= ,D为CB延长线上一点,且BD=2AB.求AD的长
,D为CB延长线上一点,且BD=2AB.求AD的长
图为抛物线 的一部分,它经过A
的一部分,它经过A ,B
,B 两点.
两点.
(1)求抛物线的解析式;
(2)将此抛物线向左平移3个单位,再向下平移1个单位,求平移后的抛物线的解析式.
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(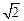 取1.414,
取1.414,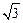 取1.732)
取1.732)
对于抛物线 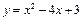 .
.
(1)它与x轴交点的坐标为 ,与y轴交点的坐标为 ,顶点坐标为 ;
(2)在坐标系中利用描点法画出此抛物线; 
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
(3)利用以上信息解答下列问题:若关于x的一元二次方程 (t为实数)在
(t为实数)在 <x<
<x<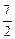 的范围内有解,则t的取值范围是 .
的范围内有解,则t的取值范围是 .
已知:如图,在△ABC中,AB="AC=" 5,BC= 8,D,E分别为BC,AB边上一点,∠ADE=∠C.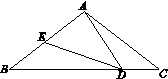
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.
两个长为2,宽为1的矩形ABCD和矩形EFGH如图1所示摆放在直线l上,DE=2,将矩形ABCD绕点D顺时针旋转 角(
角( ) ,将矩形EFGH绕点E逆时针旋转相同的角度.
) ,将矩形EFGH绕点E逆时针旋转相同的角度.
(1)当两个矩形旋转到顶点C,F重合时(如图2),∠DCE=" " °,点C到直线l的距离等于 , =" " °;(2)利用图3思考:在旋转的过程中,矩形ABCD和矩形EFGH重合部分为正方形时,
=" " °;(2)利用图3思考:在旋转的过程中,矩形ABCD和矩形EFGH重合部分为正方形时, =" " °.
=" " °.
已知:如图,AB是⊙O的直径,AC是弦,OD⊥AC于点E,交⊙O于点F,连接BF,CF,∠D=∠BFC. 
(1)求证:AD是⊙O的切线;
(2)若AC=8,tanB = ,求AD的长.
,求AD的长.
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
证明:∵ ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,
(a ≠ 0)上不同的两点,
 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.已知关于x的一元二次方程  .(其中m为实数)
.(其中m为实数)
(1)若此方程的一个非零实数根为k,
① 当k = m时,求m的值;
② 若记 为y,求y与m的关系式;
为y,求y与m的关系式;
(2)当 <m<2时,判断此方程的实数根的个数并说明理由
<m<2时,判断此方程的实数根的个数并说明理由
已知抛物线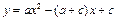 (其中a ≠ c且a ≠0).
(其中a ≠ c且a ≠0).
(1)求此抛物线与x轴的交点坐标;(用a,c的代数式表示)
(2)若经过此抛物线顶点A的直线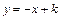 与此抛物线的另一个交点为
与此抛物线的另一个交点为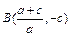 ,
,
求此抛物线的解析式;
(3)点P在(2)中x轴上方的抛物线上,直线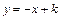 与 y轴的交点为C,若
与 y轴的交点为C,若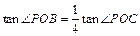 ,求点P的坐标;
,求点P的坐标;
(4)若(2)中的二次函数的自变量x在n≤x<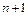 (n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .
(n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 .

 与|b+1|互为相反数,则的值为b-a=( )
与|b+1|互为相反数,则的值为b-a=( )



 ②
② ③
③ =-3 ④
=-3 ④ ⑤
⑤
 数y=mx+n与正比例函数y=mnx(m、n是常数且mn≠0)图象是( )
数y=mx+n与正比例函数y=mnx(m、n是常数且mn≠0)图象是( )
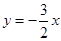 的图象是一条过原点(0,0)及点(2, )的直线
的图象是一条过原点(0,0)及点(2, )的直线
 加一个条件使△ABC≌△BAD,你的添加条件是
加一个条件使△ABC≌△BAD,你的添加条件是 
 的算术平方根是
的算术平方根是  则x+y=
则x+y= 
 .
.  ≌
≌

 的对称轴为( ).
的对称轴为( ).



 化成
化成 的形式为( ).
的形式为( ).




 有实数根.
有实数根. 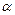 角(
角(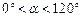 且
且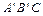 ,
,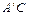 边与AB所在直线交于点D,过点 D作DE∥
边与AB所在直线交于点D,过点 D作DE∥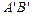 交
交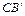 边于点E,连接BE.
边于点E,连接BE.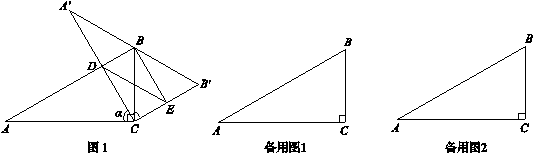
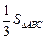
 与⊙E的位置关系.
与⊙E的位置关系. 粤公网安备 44130202000953号
粤公网安备 44130202000953号