已知关于x的一元二次方程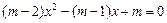 
.（其中m为实数）
（1）若此方程的一个非零实数根为k，
① 当k = m时，求m的值；
② 若记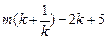
为y，求y与m的关系式；
（2）当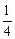
＜m＜2时，判断此方程的实数根的个数并说明理由
，
，试说明：
∥
．
，其中
相关知识点
推荐套卷
已知关于x的一元二次方程 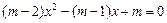.（其中m为实数）
（1）若此方程的一个非零实数根为k，
① 当k = m时，求m的值；
② 若记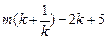为y，求y与m的关系式；
（2）当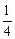＜m＜2时，判断此方程的实数根的个数并说明理由
粤公网安备 44130202000953号