已知抛物线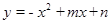经过点A（1，0）,B（6，0）.（1）求抛物线的

已知抛物线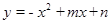经过点A （1，0）, B（6，0）.
（1）求抛物线的解析式；
（2）当y＜0,直接写出自变量x的取值范围．
（3）抛物线与y轴交于点D， P是x轴上一点，且△PAD是以AD为腰的等腰三角形，试求P点坐标。

登录免费查看答案和解析

相关试题

如图，抛物线 $y = a x^{2} + bx + 3$ 交 $x$ 轴于 $A (3, 0)$ ， $B (- 1, 0)$ 两点，交 $y$ 轴于点 $C$ ，动点 $P$ 在抛物线的对称轴上．

（1）求抛物线的解析式；

（2）当以 $P$ ， $B$ ， $C$ 为顶点的三角形周长最小时，求点 $P$ 的坐标及 $ΔPBC$ 的周长；

（3）若点 $Q$ 是平面直角坐标系内的任意一点，是否存在点 $Q$ ，使得以 $A$ ， $C$ ， $P$ ， $Q$ 为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点 $Q$ 的坐标；若不存在，请说明理由．

收藏答案/解析

已知 $ΔAOB$ 和 $ΔMON$ 都是等腰直角三角形 $(\frac{\sqrt{2}}{2} OA < OM < OA)$ ， $∠ AOB = ∠ MON = 90 °$ ．

（1）如图1，连接 $AM$ ， $BN$ ，求证： $AM = BN$ ；

（2）将 $ΔMON$ 绕点 $O$ 顺时针旋转．

①如图2，当点 $M$ 恰好在 $AB$ 边上时，求证： $A M^{2} + B M^{2} = 2 O M^{2}$ ；

②当点 $A$ ， $M$ ， $N$ 在同一条直线上时，若 $OA = 4$ ， $OM = 3$ ，请直接写出线段 $AM$ 的长．

收藏答案/解析

如图， $AB$ 是 $⊙ O$ 的直径，过点 $A$ 作 $⊙ O$ 的切线 $AC$ ，点 $P$ 是射线 $AC$ 上的动点，连接 $OP$ ，过点 $B$ 作 $BD / / OP$ ，交 $⊙ O$ 于点 $D$ ，连接 $PD$ ．

（1）求证： $PD$ 是 $⊙ O$ 的切线；

（2）当四边形 $POBD$ 是平行四边形时，求 $∠ APO$ 的度数．

收藏答案/解析

为做好新冠疫情的防控工作，某单位需购买甲、乙两种消毒液，经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元，该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液．

（1）求甲、乙两种消毒液的零售价分别是每桶多少元？

（2）由于疫情防控进入常态化，该单位需再次购买两种消毒液共300桶，且甲种消毒液的桶数不少于乙种消毒液桶数的 $\frac{1}{3}$ ．由于购买量大，甲、乙两种消毒液分别获得了20元 $/$ 桶、15元 $/$ 桶的批发价．求甲种消毒液购买多少桶时，所需资金总额最少？最少总金额是多少元？

收藏答案/解析

暑期将至，某校组织学生进行"防溺水"安全知识竞赛，老师从中随机抽取了部分学生的成绩（得分取整数，满分为100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．

其中 $A$ 组的频数 $a$ 比 $B$ 组的频数 $b$ 小15．请根据以上信息，解答下列问题：

（1）本次共抽取　　名学生， $a$ 的值为　　；

（2）在扇形统计图中， $n =$ 　　， $E$ 组所占比例为　　 $%$ ；

（3）补全频数分布直方图；

（4）若全校共有1500名学生，请根据抽样调查的结果，估计成绩在80分以上的学生人数．

收藏答案/解析