甘肃省成县苇子沟学校初二上学期期中考试数学卷
数学家发明了一个魔术盒,当任意数对 放入其中时,会得到一个新的数:
放入其中时,会得到一个新的数: .例如把
.例如把 放入其中,就会得到
放入其中,就会得到 .现将数对
.现将数对 放入其中得到数m=_________,再将数对
放入其中得到数m=_________,再将数对 放入其中后,得到的数是_______.
放入其中后,得到的数是_______.
(本题7分)“十、一”黄金周期间,园博苑在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
| 日期 |
10月1日 |
10月2日 |
10月3日 |
10月4日 |
10月5日 |
10月6日 |
10月7日 |
| 人数变化 单位:千人 |
+1.6 |
+0.8 |
+0.4 |
-0.4 |
-0.8 |
+0.2 |
-1.2 |
(1)若9月30日的游客人数记为a,请用a的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)若9月30日的游客人数为5千人,门票每人60元.问黄金周期间园博苑门票收入是多少元?
挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式——阿贝尔公式:下图是一个简单的阶梯形,可用两种方法,每一种把图形分割成为两个矩形.利用它们之间的面积关系,可以得到: =( )
=( )
A. |
B. |
C. |
D. |
下图是行列间隔都为1个单位的点阵:
①你能计算点阵中多边形的面积吗?请将答案直接填入图中横线上。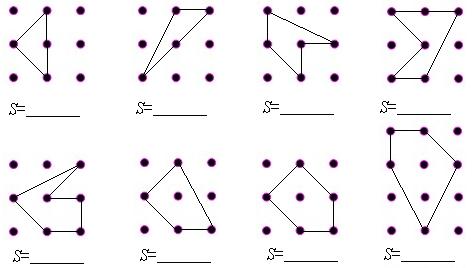
②若用a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积,你能用含a和b的代数式表示S= ____________________
③请你利用②中的公式来求a=4,b=20时,多边形的面积S。
二次函数 的图象可由
的图象可由 的图象()
的图象()
| A.向左平移1个单位,再向下平移2个单位得到 |
| B.向左平移1个单位,再向上平移2个单位得到 |
| C.向右平移1个单位,再向下平移2个单位得到 |
| D.向右平移1个单位,再向上平移2个单位得到 |
如图,点A、B的坐标分别为(1, 4)和(4, 4),一条抛物线与x轴交于C、D两点(C在D的左侧),它的顶点可在线段AB上运动,在运动过程中点C的横坐标最小值为 ,则点D的横坐标最大值为 ( )
,则点D的横坐标最大值为 ( )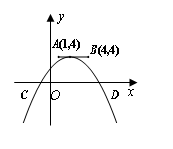
A.-3 B.1 C.5 D.8
嫦娥二号探月卫星于2010年10月1日发射成功。某科技实验小组也自行设计了火箭,经测试,该种火箭被竖直向上发射时,它的高度h (m)与时间t (s)的关系可以用公式 表示.经过______s,火箭达到它的最高点.
表示.经过______s,火箭达到它的最高点.
满足下列哪种条件时,能够判定△ABC≌△DEF
| A.AB=DE,BC=EF,∠A=∠E | B.AB=DE,BC=EF,∠A=∠D |
| C.∠A=∠E,AB=DF,∠B=∠D | D.∠A=∠D,AB=DE,∠B=∠E |
在下列各数中: 3.1415926,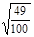 ,0.2,
,0.2,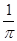 ,
,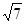 ,
,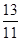 ,
, 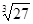 ,无理数的个数是
,无理数的个数是
| A.2 | B.3 | C.4 | D.5 |
等腰三角形中,有一内角为40°,则它的另外两个内角分别是
| A.40°、50° | B.40°、80° | C.40°、100°或70°、70° | D.40°、100° |
已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b))2003的值为
| A.0 | B.-1 | C.1 | D.(-3)2003 |
如图1,△ABC中,AB=AC,三条高AD,BE,CF相交于O,那么图中全等的三角形有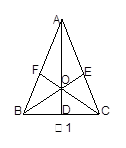
| A.5对 | B.6对 | C.7对 | D.8对 |
如图2,E是△ABC边BC上的一点,DE垂直平分AB,△ACE的周长是8.5,AB=3,则△ABC的周长为
| A.8.5 | B.10 | C.11.5 | D.13 |
下列说法中,正确的是
| A.实数-a2是负数 | B. =|a| =|a| |
C.|-a|一定是正数 | D.实数-a的绝对值是a |
如图3,∠AOP=∠BOP=15°,PC∥OA,若PC=4,则PD等于
| A.1 | B.3 | C.4 | D.2 |
平方根等于本身的数是______________,立方根等于本身的数是___________,所有正整数的平方根的和等于_____________
已知点P为∠AOB的角平分线上的一点,它到OA的距离为2 cm,那么它到OB的距离是________
如图4,已知在△ABC和△ADCB中,AC=DB,若不增加任何字母与辅助线,要使△ABC≌△DCB,则还需增加一个条件是_________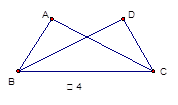
如图5,在△ABC中,已知∠ABC和∠ACB的角平分线相交于F,经过F作DE∥BC交AB于点D,交AC于点E,若BD+CE=9,则线段DE的长为____________
小明设计了一个关于实数运算的程序,输入一个数后,输出的数总是比该数的平方小1,小明按照此程序输入 后,输出的结果应为______
后,输出的结果应为______
如图6,已知△ABC的周长是21,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是_________
如图7,已知P、Q是△ABC的边BC上的两点,且BP=QC=PQ=AP=AQ,则∠BAC=________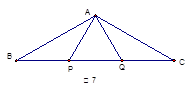
某地有两座工厂和两条交叉的公路,图中点M、N表示工厂,OA、OB表示公路,现计划修建一座物资仓库,希望仓库到两工厂的距离相同,到两条公路的的距离相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计。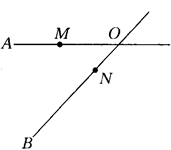
(尺规作图,不写作法,保留作图痕迹)
如图8,已知点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF,求证:△ABC≌△DEF。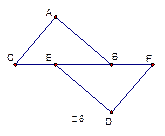
如图11,AD是△ABC的角平分线,DE、DF分别是△ABD和△AC D的高,求证:AD垂直平分EF。(5分)
D的高,求证:AD垂直平分EF。(5分)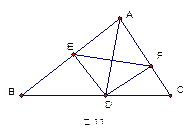
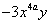 与
与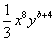 的和是一个单项式,则
的和是一个单项式,则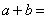 _________________,它们的和为__________________.
_________________,它们的和为__________________. 的次数是______次,把它按字母c升幂排列的结果是________________________.
的次数是______次,把它按字母c升幂排列的结果是________________________. 的和是
的和是 ,则这个多项式是______.
,则这个多项式是______.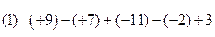
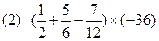
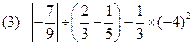

 作出解释.
作出解释. 表示在数轴上,并将它们按从小到大的顺序排列
表示在数轴上,并将它们按从小到大的顺序排列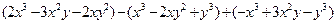 的值,其中
的值,其中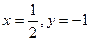 ”。甲同学把“
”。甲同学把“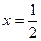 ”错抄成“
”错抄成“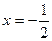 ”,但他计算的结果也是正确的,试说明理由,并求出这个结果.
”,但他计算的结果也是正确的,试说明理由,并求出这个结果.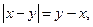 且
且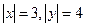 ,试求
,试求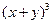 的值
的值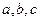 满足
满足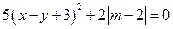 ;②
;②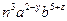 是一个三次单项式且系数为-1:
是一个三次单项式且系数为-1: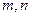 的值; (2)求代数式
的值; (2)求代数式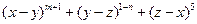 的值.
的值.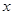 表示一个两位数,
表示一个两位数,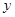 也表示一个两位数,小明想用
也表示一个两位数,小明想用
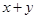
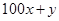
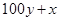
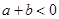 ,
,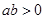 那么这两个数 ( )
那么这两个数 ( ) 、
、 互为相反数,且
互为相反数,且 ,
, 、
、 互为倒数,
互为倒数, 为立方等于本身的有理数,
为立方等于本身的有理数, 为正整数,则
为正整数,则 =________;
=________;
 ;
; =_____________.
=_____________.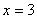 时,代数式
时,代数式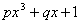 的值为2008,则当
的值为2008,则当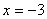 时,代数式
时,代数式



 有两个不相等的实数根,则
有两个不相等的实数根,则 满足的条件是()
满足的条件是()  上的一个点是()
上的一个点是() 的图象如图所示,则一次函数
的图象如图所示,则一次函数 的
的 是方程
是方程 的两根,则
的两根,则 ()
() 的一元二次方程的一个根是1,写出一个符合条件的方程:
的一元二次方程的一个根是1,写出一个符合条件的方程:  的图象经过原点,与x轴的另一个交点为A, 抛物线的顶点为B,则△OAB的面积为
的图象经过原点,与x轴的另一个交点为A, 抛物线的顶点为B,则△OAB的面积为 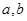 为实数,且
为实数,且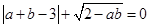 ,则以
,则以

 )2
)2 的平方根是____________
的平方根是____________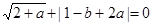 ,则2a+3b=_____
,则2a+3b=_____
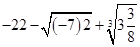
 求
求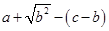 的值
的值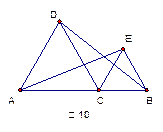




 DE⊥AB于E,DF⊥AC于点F,且BE=CF,求证AD⊥BC。
DE⊥AB于E,DF⊥AC于点F,且BE=CF,求证AD⊥BC。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号