2011年南京市下关区秦淮区沿江区中考数学一模试卷
如图,从边长为(a+3)cm的正方形纸片中剪去一个边长为3cm的正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为acm,则另一边长是( ▲ )
| A.(2 a+3)cm | B.(2 a+6)cm |
| C.(2a+3)cm | D.(a+6)cm |
2010年上海世界博览会,中国馆投资1095600000元,将1095600000保留两个
有效数字的近似数应为_____ ▲__ 元.
某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是 ▲ .(把所有正确答案的序号填写在横线上).
①1~2月份利润的增长快于2~3月份利润的增长;
②1~4月份利润的极差与1~5月份利润的极差相同;
③1~5月份利润的众数是130万元;
④1~5月份利润的中位数是120万元.
统计2010年上海世博会前20天日参观人数,得到如下频数分布表和频
数分布直方图(部分未完成):


(1)请补全频数分布表和频数分布直方图;
(2)求出日参观人数不低于22万的天数所占的百分比;
(3)利用以上信息,试估计上海世博会(会期184天)的参观总人数.
如图,南京绿博园中有一条人工河,河的两岸PQ、MN互相平行,河 岸PQ上有一排间隔为50米的彩灯柱C、D、E、……,某人在河岸MN的A处测得∠DAN=21º,然后沿河岸走了175米到达B处,测得∠CBN=45º,求这条河的宽度.(参考数据:
岸PQ上有一排间隔为50米的彩灯柱C、D、E、……,某人在河岸MN的A处测得∠DAN=21º,然后沿河岸走了175米到达B处,测得∠CBN=45º,求这条河的宽度.(参考数据: ,
, )
)

为了庆祝六一儿童节,某食品厂制作了3种不同的精美卡片,每袋食品随机装入一张卡片,集齐三种卡片可获奖,现购买该种食品3袋,能获奖的概率是多少?
.(6分) 已知二次函数 的图象与y轴交于点A(0,-6),与x轴的一个交点坐标是B(-2,0).
的图象与y轴交于点A(0,-6),与x轴的一个交点坐标是B(-2,0).
(1)求二次函数的关系式,并写出顶点坐标;
(2)将二次函数图象沿x轴向左平移 个单位长度,求所得图象对应的函数关系式.
个单位长度,求所得图象对应的函数关系式.
如图,已知线段 是
是 的中点,直线
的中点,直线 于点
于点 ,直线
,直线 于点
于点 ,点
,点 是
是 左侧一点,
左侧一点, 到
到 的距离为
的距离为
(1)画出点 关于
关于 的对称点
的对称点 ,并在
,并在 上取一点
上取一点 ,使点
,使点 、
、 关于
关于 对称;
对称;
(保留画图痕迹,不要求写画法)
(2) 与
与 有何位置关系和数量关系?请说明理由.
有何位置关系和数量关系?请说明理由.
如图, 内接于⊙
内接于⊙ ,点
,点 在半径
在半径 的延长线上,
的延长线上, .
.
(1)判断直线 与⊙
与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙ 的半径长为1,求由弧
的半径长为1,求由弧 、线段
、线段 和
和 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留 和根号).
和根号).
甲乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留半小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为60km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下.
(1)将图中( )填上适当的值,并求甲车从A到B的速度.
(2)求从甲车返回到与乙车相遇过程中y与x的函数关系式,并写出自变量取值范围.
(3)求出甲车返回时行驶速度及AB两地的距离.
(10分)某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.
(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共l00个,设做竖式纸盒x个.
① 根据题意,完成以下表格:
 纸盒 纸盒纸板 |
竖式纸盒(个) |
横式纸盒(个) |
 x x |
100-x |
|
| 正方形纸板(张) |
▲ |
2(100-x) |
| 长方形纸板(张) |
4x |
▲ |
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述 两种纸盒,纸板恰好用完.已知290<a<306.求 a的值.
两种纸盒,纸板恰好用完.已知290<a<306.求 a的值.
如图,已知直角梯形ABCD中,AD//BC, DC⊥BC,AB=5,BC=6, ∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
(1)当BO=AD时,求BP的长;
(2)在点O运动的 过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
(3)在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围.
(参考数据:cos5 3°≈0.6;sin53°≈0.8;t
3°≈0.6;sin53°≈0.8;t an74°
an74° 3.5)
3.5)
如图甲所示,将长为30cm,宽为2cm的长方形白纸条,折成图乙所示的图形并在其一面着色,则着色部分的面积为
| A.60cm2 | B.58 cm2 | C.56 cm2 | D.54 cm2 |
甲、乙两人5次射击命中的环数如下:
| 甲 |
7 |
9 |
8 |
6 |
10 |
| 乙 |
7 |
8 |
9 |
8 |
8 |
则以下判断中正确的是( ▲ )
A. 甲=
甲= 乙,S甲2=S乙2 B.
乙,S甲2=S乙2 B. 甲=
甲= 乙,S甲2>S乙2
乙,S甲2>S乙2
C. 甲=
甲= 乙,S甲2 <S乙2 D.
乙,S甲2 <S乙2 D. 甲<
甲< 乙,S甲2<S乙2
乙,S甲2<S乙2
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半
径为3cm,则圆心O到弦CD的距离为( ▲ )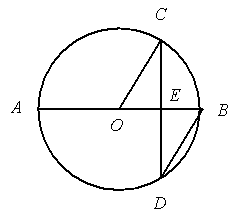
A.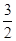 cm cm |
B.3 cm | C.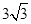 cm cm |
D.6cm |
将矩形纸片ABCD按如图所示的方式折叠,得到 菱形AECF.若AB=6,则BC的长为( ▲ )
菱形AECF.若AB=6,则BC的长为( ▲ ) 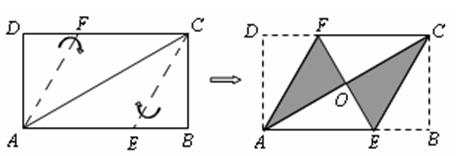
| A.1 | B.2 |
C.2 |
D.12 |
校篮球队进行1分钟定点投篮测试, 10名队员投中的球数由小到大
排序的结果为7、8、9、9、9、10、10、10、10、12,则这组数据的中位数是 ▲ .
不透明的袋子里装有将10个乒乓球,其中5个白色的,2个黄色的,3
个红色的,这些乒乓球除颜色外全相同,从中任意摸出一个,则摸出白色乒乓球的
概率是 ▲ .
如图,平行四边形ABCD中,AD=5cm,AB⊥BD,点O是两条对角
线的交点,OD=2,则AB= ▲ cm.
全国两会期间,温家宝总理强调,“十二五”期间,将新建保障性住房
36 000 000套.这些住房将有力地缓解住房的压力,特别是解决中低收入和新参加
工作的大学生住房的需求.把36 000 000用科学记数法表示应是 ▲ .
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下
表:
| x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
… |
| y |
… |
3 |
-2 |
-5 |
-6 |
-5 |
… |
则x<-2时, y的取值范围是 ▲ .
如图,平行四边形ABCD中,∠ABC=60°,AB=4,AD=8,点E、F
分别是边BC、AD边的中点,点M是AE与BF的交点,点N是CF与DE的交点,
则四边形ENFM的周长是 ▲ .
如图,正方形ABCD中,点E在边AB上,点G在边AD上,且∠ECG
=45°,点F在边AD的延长线上,且DF= BE.则下列结论:①∠ECB是锐角,;
②AE<AG;③△CGE≌△CGF;④EG= BE+GD中一定成立的结论有 ▲
(写出全部正确结论).
(6分)如图,已知,四边形ABCD为梯形,分别过点A、D作底边BC
的垂线,垂足分别为点E、F.四边形ADFE是何种特殊的四边形?请写出你的理
由.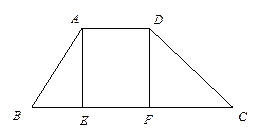
.(6分)在直角坐标平面内,二次函数y=ax2+bx-3(a≠0)图象的顶点为
A(1,-4).
(1)求该二次函数关系式;
(2)将该二次函数 图象向上平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与
图象向上平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与 轴的另一个交点的坐标.
轴的另一个交点的坐标.
(6分) 某中学组织全体学生参加了“喜迎青奥,走出校门,服务社会”的
活动.该中学以九年级(2)班为样本,统计了该班学生宣传青奥,打扫街道,去敬
老院服务和在十字路口值勤的人数,并做了如下直方图和扇形统计图(A~宣传青
奥;B~打扫街道;C~去敬老院服务;D~在十字路口值勤).
(1)求去敬老院服务对应的扇形圆心角的度数;
(2)若该中学共有800学生,请估计这次活动中在十字路口值勤的学生共有多少人?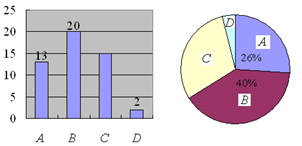
(6分) “五一劳动节大酬宾!”,某家具城设计的促销活动如下:在一个
不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50
元”的字样.规定:在本商场同一日内,顾客每消费满500元,就可以在箱子里先
后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格
的购物券,购物券可以在本商场消费.某顾客刚好消费500元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
(8分)已知以下基本事实:①对顶角相等;②一条直线截两条平行直线
所得的同位角相等;③两条直线 被第三条直线所截,若同位角相等,则这两条直线
被第三条直线所截,若同位角相等,则这两条直线
平行;④全等三角形的对应边、对应角分别相等.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有 (填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”.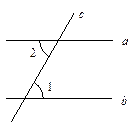
已知:如图,_________________________________.
求证:_________________________________.
证明:
(8分)如图,小岛在港口P的北偏西60°方向,距港口56海里的A处,
货船从港口P出发,沿北偏东45°方向匀速驶离港口P,4小时后货船在小岛的正
东方向.求货船的航 行速度.(精确到0.1海里/时,参考数据:
行速度.(精确到0.1海里/时,参考数据: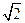 ≈1.41,
≈1.41,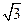 ≈1.73)
≈1.73)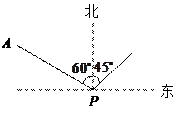
(8分)某经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,
月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该
经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查
发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)填空:当每吨售价是240元时,此时的月销售量是 吨;
(2)该经销店计划月利润为9000元而且尽可能地扩大销售量,则售价应定为每吨多少元?
(10分)如图直角坐标系中,已知A(-4,0),B(0,3),点M在线段A
上.
(1)如图1,如果点M是线段AB的中点,且⊙M的半径为2,试判断直线OB与⊙M的位置关系 ,并说明理由;
,并说明理由;
(2)如图2,⊙M与x轴、y轴都相切,切点分别是点E、F,试求出点M的坐标.
(8分) (1)学习《测量建筑物的高度》后,小明带着卷尺、标 杆,利用太
杆,利用太
阳光去测量旗杆的高度.
参考示意图1,他的测量方案如下:
第一步,测量数据.测出CD=1.6米,CF=1.2米, AE=9米.
第二步,计算.
请你依据小明的测量方案计算出旗杆的高度.
(2) 如图2,校园内旗杆周围有护栏,下面有底座.现在有卷尺、标杆、平面镜、测角仪等工具,请你选择 出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
要求:在备 用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
你选择出的必须工具是 ;
需要测量的数据是 .
 的解是 ▲ .
的解是 ▲ . 中自变量x的取值范围是 ▲ .
中自变量x的取值范围是 ▲ .

 __▲___.
__▲___.
 的图像经过第 ▲ 象限.
的图像经过第 ▲ 象限.
 ,再从0,
,再从0, , 2,1中选择一
, 2,1中选择一 和
和 中,
中, 、
、 交于点M.
交于点M.
 交
交 于点N,四边形BNCM是什么四边形?请证明你的结论.
于点N,四边形BNCM是什么四边形?请证明你的结论.





 ,则a2-b2-2b+1的值为
,则a2-b2-2b+1的值为 
 有意义的x的取值范围是( ▲ )
有意义的x的取值范围是( ▲ )
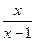 -
-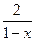 )÷
)÷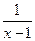 ,其中x=
,其中x=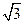 +1.
+1.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号