初中数学命题与定理试题

下列语句正确的是 $($　　 $)$

A．对角线互相垂直的四边形是菱形

B．有两边及一角对应相等的两个三角形全等

C．矩形的对角线相等

D．平行四边形是轴对称图形

定理：三角形的一个外角等于与它不相邻的两个内角的和．

已知：如图， $\angle \mathit{ACD}$ 是 $\mathit{\Delta ABC}$ 的外角．求证： $\angle \mathit{ACD}=\angle A+\angle B$ ．

证法1：如图， $\because \angle A+\angle B+\angle \mathit{ACB}=180°$ （三角形内角和定理）， 又     $\because \angle \mathit{ACD}+\angle \mathit{ACB}=180°$ （平角定义）， $\therefore \angle \mathit{ACD}+\angle \mathit{ACB}=\angle A+\angle B+\angle \mathit{ACB}$ （等量代换）． $\therefore \angle \mathit{ACD}=\angle A+\angle B$ （等式性质）．

证法2：如图， $\because \angle A=76°$ ，     $\angle B=59°$ ， 且     $\angle \mathit{ACD}=135°$ （量角器测量所得） 又     $\because 135°=76°+59°$ （计算所得） $\therefore \angle \mathit{ACD}=\angle A+\angle B$ （等量代换）．

下列说法正确的是 $($ 　　 $)$

A．	证法1还需证明其他形状的三角形，该定理的证明才完整
B．	证法1用严谨的推理证明了该定理
C．	证法2用特殊到一般法证明了该定理
D．	证法2只要测量够一百个三角形进行验证，就能证明该定理

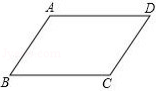
平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．

已知：如图，在四边形 $\mathit{ABCD}$中， $\mathit{AB}=\mathit{CD}$， $\mathit{AD}=\mathit{BC}$．

求证：四边形 $\mathit{ABCD}$是平行四边形．

证明：

下列命题中的真命题是 $($　　 $)$

①相等的角是对顶角 ②矩形的对角线互相平分且相等 ③垂直于半径的直线是圆的切线 ④顺次连接四边形各边中点所得四边形是平行四边形．

A．①②B．②③C．③④D．②④

数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是 　　（只填写序号）．

①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了"两点确定一条直线"；

②车轮做成圆形，应用了"圆是中心对称图形"；

③学校门口的伸缩门由菱形而不是其他四边形组成，应用了"菱形的对角线互相垂直平分"；

④地板砖可以做成矩形，应用了"矩形对边相等"．

下列命题中，是真命题的是 $($　　 $)$

A．有一个角是直角的四边形是矩形

B．对角线相等的四边形是矩形

C．一组邻边相等的四边形是菱形

D．对角线互相垂直平分的四边形是菱形

下列命题是真命题的是 $($　　 $)$

A．四边都相等的四边形是矩形

B．菱形的对角线相等

C．对角线互相垂直的平行四边形是正方形

D．对角线相等的平行四边形是矩形

下列命题中假命题是 $($　　 $)$

A．正六边形的外角和等于 $360°$

B．位似图形必定相似

C．样本方差越大，数据波动越小

D．方程 $x^2+x+1=0$无实数根

下列说法正确的是 $($　　 $)$

A．圆内接正六边形的边长与该圆的半径相等

B．在平面直角坐标系中，不同的坐标可以表示同一点

C．一元二次方程 $a{x}^2+\mathit{bx}+c=0(a\ne 0)$一定有实数根

D．将 $\mathit{\Delta ABC}$绕 $A$点按顺时针方向旋转 $60°$得 $\mathit{\Delta ADE}$，则 $\mathit{\Delta ABC}$与 $\mathit{\Delta ADE}$不全等

下列命题正确的是 $($　　 $)$

A．对角线相等的四边形是平行四边形

B．对角线相等的四边形是矩形

C．对角线互相垂直的平行四边形是菱形

D．对角线互相垂直且相等的四边形是正方形

下列命题：①若 $a<1$，则 $(a-1)\sqrt{\frac{1}{1-a}}=-\sqrt{1-a}$；②平行四边形既是中心对称图形又是轴对称图形；③ $\sqrt{9}$的算术平方根是3；④如果方程 $a{x}^2+2x+1=0$有两个不相等的实数根，则实数 $a<1$．其中正确的命题个数是 $($　　 $)$

A．1个B．2个C．3个D．4个

对于命题“若 $a^2>b^2$，则 $a>b$”，下面四组关于 $a$， $b$的值中，能说明这个命题是假命题的是 $($　　 $)$

A． $a=3$， $b=2$B． $a=-3$， $b=2$C． $a=3$， $b=-1$D． $a=-1$， $b=3$

下列关于函数 $y=x^2-6x+10$的四个命题：

①当 $x=0$时， $y$有最小值10；

② $n$为任意实数， $x=3+n$时的函数值大于 $x=3-n$时的函数值；

③若 $n>3$，且 $n$是整数，当 $n⩽x⩽n+1$时， $y$的整数值有 $(2n-4)$个；

④若函数图象过点 $(a,y_0)$和 $(b,y_0+1)$，其中 $a>0$， $b>0$，则 $a<b$．

其中真命题的序号是 $($　　 $)$

A．①B．②C．③D．④

下列命题是真命题的是 $($　　 $)$

A．三个角相等的平行四边形是矩形

B．对角线相等的四边形是矩形

C．平行四边形的对角线互相垂直

D．对角线互相垂直的四边形是菱形

下列命题是真命题的是 $($　　 $)$

A．三个角相等的平行四边形是矩形

B．对角线相等的四边形是矩形

C．平行四边形的对角线互相垂直

D．对角线互相垂直的四边形是菱形