如图,在平面直角坐标系 中, , , , 是 的内心,将 绕原点逆时针旋转 后, 的对应点 的坐标为
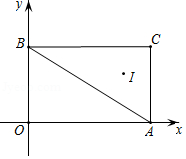
A. B. C. D.
如图,矩形 中, , ,连接 , 和 分别是 和 的内切圆,则 的长是

A. B. C. D.
如图,,点
、
分别在射线
、
上,
,
.
(1)用尺规在图中作一段劣弧,使得它在、
两点分别与射线
和
相切.要求:写出作法,并保留作图痕迹;
(2)根据(1)的作法,结合已有条件,请写出已知和求证,并证明;
(3)求所得的劣弧与线段、
围成的封闭图形的面积.

已知关于的一元二次方程
.
(1)求证:无论为任何实数,此方程总有两个实数根;
(2)若方程的两个实数根为、
,满足
,求
的值;
(3)若的斜边为5,另外两条边的长恰好是方程的两个根
、
,求
的内切圆半径.
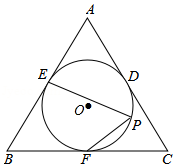
已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

阅读以下材料,并按要求完成相应的任务:
莱昂哈德欧拉
是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面就是欧拉发现的一个定理:在
中,
和
分别为外接圆和内切圆的半径,
和
分别为其中外心和内心,则
.

如图1,和
分别是
的外接圆和内切圆,
与
相切分于点
,设
的半径为
,
的半径为
,外心
(三角形三边垂直平分线的交点)与内心
(三角形三条角平分线的交点)之间的距离
,则有
.
下面是该定理的证明过程(部分)
延长交
于点
,过点
作
的直径
,连接
,
.
,
(同弧所对的圆周角相等).
.
,
,①
如图2,在图1(隐去,
的基础上作
的直径
,连接
,
,
,
.
是
的直径,所以
.
与
相切于点
,所以
,
.
(同弧所对的圆周角相等),
,
.
②
任务:(1)观察发现:,
(用含
,
的代数式表示);
(2)请判断和
的数量关系,并说明理由.
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若的外接圆的半径为
,内切圆的半径为
,则
的外心与内心之间的距离为
.
如图,在 中, , ,点 是 边上的一点, ,设 与 的内切圆半径分别为 , ,那么

A.2B. C. D.
如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
A. B. C. D.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

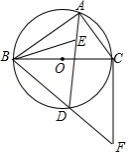
如图, 是 的外接圆, 为 的直径,点 为 的内心,连接 并延长交 于 点,连接 并延长至 ,使得 ,连接 、 .
(1)求证: ;
(2)求证:直线 为 的切线.