我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
(2)如图, 中, ,点 在 上,且 ,求证: 是 的“内似线”;
(3)在 中, , , , 、 分别在边 、 上,且 是 的“内似线”,求 的长.

如图,四边形 内接于 ,点 是 的内心, ,点 在 的延长线上,则 的度数为
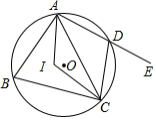
A. B. C. D.
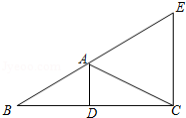
如图,在 中, 是边 上的中线, , , 交 的延长线于点 , , .
(1)求 的长;
(2)求证: 为等腰三角形.
(3)求 的外接圆圆心 与内切圆圆心 之间的距离.
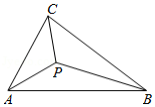
如图, 是 的内心,连接 、 、 , 、 、 的面积分别为 、 、 .则 .(填“ ”或“ ”或“ ”
如图,在平面直角坐标系 中, , , , 是 的内心,将 绕原点逆时针旋转 后, 的对应点 的坐标为
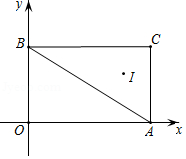
A. B. C. D.
如图,矩形 中, , ,连接 , 和 分别是 和 的内切圆,则 的长是

A. B. C. D.
已知 的内切圆 与 、 、 分别相切于点 、 、 ,若 ,如图1.
(1)判断 的形状,并证明你的结论;
(2)设 与 相交于点 ,如图2, ,求 的长.

如图,在 中, , , 、 分别在 、 上,点 在 内.若四边形 是边长为1的正方形,则 .

如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
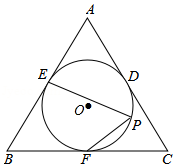
A. B. C. D.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

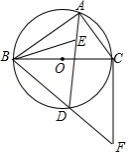
如图, 是 的外接圆, 为 的直径,点 为 的内心,连接 并延长交 于 点,连接 并延长至 ,使得 ,连接 、 .
(1)求证: ;
(2)求证:直线 为 的切线.