初中数学切线的性质试题

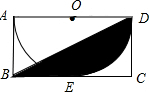
如图，矩形 ABCD中， BC＝4， CD＝2，以 AD为直径的半圆 O与 BC相切于点 E，连接 BD，则阴影部分的面积为 　．（结果保留π）

如图， $\mathit{PA}$ 、 $\mathit{PB}$ 分别与 $\odot O$ 相切于 $A$ 、 $B$ ， $\angle P=70°$ ， $C$ 为 $\odot O$ 上一点，则 $\angle \mathit{ACB}$ 的度数为 $($ 　　 $)$

A．

$110°$

B．

$120°$

C．

$125°$

D．

$130°$

以 O为中心点的量角器与直角三角板 ABC如图摆放，直角顶点 B在零刻度线所在直线 DE上，且量角器与三角板只有一个公共点 P，则∠ CBD的度数是（　　）

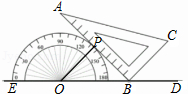
A．

45°10'

B．

44°50'

C．

46°10'

D．

不能确定

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，以 $\mathit{AB}$为直径作 $\odot O$交 $\mathit{BC}$于点 $D$，过点 $D$作 $\odot O$的切线 $\mathit{DE}$交 $\mathit{AC}$于点 $E$，交 $\mathit{AB}$延长线于点 $F$．

（1）求证： $\mathit{DE}\perp \mathit{AC}$；

（2）若 $\mathit{AB}=10$， $\mathit{AE}=8$，求 $\mathit{BF}$的长．

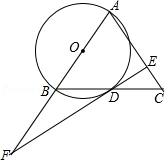
如图，⊙ O为等腰三角形 ABC的外接圆， AB是⊙ O的直径， AB＝12， P为 $\stackrel{⏜}{\mathit{BC}}$ 上任意一点（不与点 B， C重合），直线 CP交 AB的延长线于点 Q，⊙ O在点 P处的切线 PD交 BQ于点 D，则下列结论：①若∠ PAB＝30°，则 $\stackrel{⏜}{\mathit{PB}}$ 的长为π；②若 PD∥ BC，则 AP平分∠ CAB；③若 PB＝ BD，则 PD＝6 $\sqrt{3}$ ；④无论点 P在 $\stackrel{⏜}{\mathit{BC}}$ 上的位置如何变化， CP• CQ＝108．其中正确结论的序号为 　　．

如图，已知 $\mathit{AB}$为 $\odot O$直径， $\mathit{AC}$是 $\odot O$的切线，连接 $\mathit{BC}$交 $\odot O$于点 $F$，取 $\stackrel{̂}{\mathit{BF}}$的中点 $D$，连接 $\mathit{AD}$交 $\mathit{BC}$于点 $E$，过点 $E$作 $\mathit{EH}\perp \mathit{AB}$于 $H$．

（1）求证： $\mathit{\Delta HBE}\backsim \mathit{\Delta ABC}$；

（2）若 $\mathit{CF}=4$， $\mathit{BF}=5$，求 $\mathit{AC}$和 $\mathit{EH}$的长．

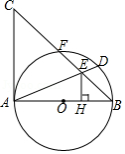
如图，在矩形中，，以顶点为圆心，1为半径作，过边上的一点作射线与相切于点，且交边于点，连接，若，，则 的大小约为　　度　　分．（参考数据： $\sin {11}^{\circ }{32}^{\text{'}}=\frac{1}{5}$， $\tan {36}^{\circ }{52}^{\text{'}}=\frac{3}{4}$）

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle C=90°$， $\mathit{AC}=4$， $\mathit{BC}=3$，点 $O$是 $\mathit{AB}$的三等分点，半圆 $O$与 $\mathit{AC}$相切， $M$， $N$分别是 $\mathit{BC}$与半圆弧上的动点，则 $\mathit{MN}$的最小值和最大值之和是 $($　　 $)$

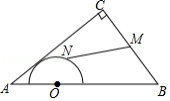
A．5B．6C．7D．8

如图， $\mathit{AB}$为 $\odot O$的切线，切点为 $A$，连接 $\mathit{AO}$、 $\mathit{BO}$， $\mathit{BO}$与 $\odot O$交于点 $C$，延长 $\mathit{BO}$与 $\odot O$交于点 $D$，连接 $\mathit{AD}$．若 $\angle \mathit{ABO}=36°$，则 $\angle \mathit{ADC}$的度数为 $($　　 $)$

A． $54°$B． $36°$C． $32°$D． $27°$

如图， $\mathit{AB}$为 $\odot O$的直径， $\mathit{BC}$、 $\mathit{CD}$是 $\odot O$的切线，切点分别为点 $B$、 $D$，点 $E$为线段 $\mathit{OB}$上的一个动点，连接 $\mathit{OD}$， $\mathit{CE}$， $\mathit{DE}$，已知 $\mathit{AB}=2\sqrt[]{5}$， $\mathit{BC}=2$，当 $\mathit{CE}+\mathit{DE}$的值最小时，则 $\frac{\mathit{CE}}{\mathit{DE}}$的值为 $($　　 $)$

A． $\frac{9}{10}$B． $\frac{2}{3}$C． $\frac{\sqrt{5}}{3}$D． $\frac{2\sqrt[]{5}}{5}$

如图，过⊙O上的两点A、B分别作切线，并交BO、AO的延长线于点C、D，连接CD，交⊙O于点E、F，过圆心O作OM⊥CD，垂足为M点．

求证：（1）△ACO≌△BDO；（2）CE＝DF．

如图， 是 的直径， ，点 为线段 上一点（不与 ， 重合），作 ，交 于点 ，垂足为点 ，作直径 ，过点 的切线交 的延长线于点 ， 于点 ，连接 ．

（1）求证： 是 的平分线；

（2）求证： ；

（3）当 $\frac{\mathit{CF}}{\mathit{CP}}=\frac{3}{4}$ 时，求劣弧 的长度（结果保留

如图，四边形 ABCD中， MA＝ MC， MB＝ MD，以 AB为直径的圆 O过点 M且与 DC延长线相切于点 E．

（1）求证：四边形 ABCD是菱形；

（2）若 AB＝4，求 $\stackrel{⏜}{\mathit{BM}}$ 的长（结果请保留π）

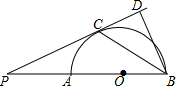
如图，AB是半圆O的直径，点P是BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC．求证：

（1）∠PBC＝∠CBD；

（2）BC²＝AB•BD．

抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一．如图， $\mathit{AC}$ ， $\mathit{BD}$ 分别与 $\odot O$ 相切于点 $C$ ， $D$ ，延长 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $P$ ．若 $\angle P=120°$ ， $\odot O$ 的半径为 $6\mathit{cm}$ ，则图中 $\stackrel{̂}{\text{CD}}$ 的长为 　　 $\mathit{cm}$ ．（结果保留 $\pi )$