初中数学圆内接四边形的性质解答题

如图，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5，在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK。
（1）若∠1=70°，求∠MKN的度数；
（2）当折痕MN与对角线AC重合时，试求△MNK的面积．
（3）△MNK的面积能否小于0．5？若能，求出此时∠1的度数；若不能，试说明理由；

（本题8分）在等腰梯形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以每秒2个单位长度的速度沿AD→DC向终点C运动，同时点Q从点B出发，以每秒1个单位的速度沿BA向终点A运动，设运动时间为t秒.
⑴当t为何值时，四边形PQBC为平行四边形时？
⑵在整个运动过程中，当t为何值时，以点C、P、Q为顶点的三角形是直角三角形？

 

如图，在平面直角坐标系中，正方形OABC的边长为a．直线y=bx+c交x轴于E，交y轴于F，且a、b、c分别满足-(a-4)²≥0，
（1）求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标；
（2）直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移，设平移的时间为t秒，问是否存在t的值，使直线EF平分正方形OABC的面积？若存在，请求出t的值；若不存在，请说明理由；
点P为正方形OABC的对角线AC上的动点（端点A、C除外），PM⊥PO，交直线AB于M，求的值

如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），
（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线
＝－＋交折线OAB于点E．
（1）记△ODE的面积为S，求S与的函数关系式；
（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形O₁A₁B₁C₁，试探究O₁A₁B₁C₁与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.

如图，在直角坐标系中，四边形OABC的OA，OC两边分别在x，y轴上，OA∥BC，BC=15cm，A点坐标为（16，0），C点坐标为（0，4）．点P，Q分别从C，A同时出发，点P以2cm/s的速度由C向B运动，点Q以4cm/s的速度由A向O运动，当点Q到达点O时，点P也停止运动，设运动时间为t秒（0≤t≤4）．

（1）求当t为多少时，四边形PQAB为平行四边形？
（2）求当t为多少时？PQ所在直线将四边形OABC分成左右两部分的面积比为1：2；
（3）直接写出在（2）的情况下，直线PQ的函数关系式．

、(本题12分)如图甲，在△ABC中，E是AC边上的一点，
(1)在图甲中，作出以BE为对角线的平行四边形BDEF，使D、F分别在BC和AB边上；
(2)改变点E的位置，则图甲中所作的平行四边形BDEF有没有可能为菱形？若有，请在图乙中作出点E的位置（用尺规作图，并保留作图痕迹）；若没有，请说明理由．

 

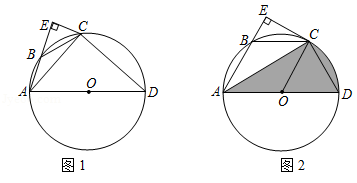
把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点B重合，联结DF，点M，N分别为DF，EF的中点，联结MA，MN．
（1）如图1，点E，F分别在正方形的边CB，AB上，请判断MA，MN的数量关系和位置关系，直接
写出结论；
（2）如图2，点E，F分别在正方形的边CB，AB的延长线上，其他条件不变，那么你在（1）中得到的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

图1                            图2

如图，在锐角三角形 $\mathit{ABC}$ 中， $\mathit{AD}$ 是 $\mathit{BC}$ 边上的高，以 $\mathit{AD}$ 为直径的 $\odot O$ 交 $\mathit{AB}$ 于点 $E$ ，交 $\mathit{AC}$ 于点 $F$ ，过点 $F$ 作 $\mathit{FG}\perp \mathit{AB}$ ，垂足为 $H$ ，交 $\stackrel{̂}{\mathit{AE}}$ 于点 $G$ ，交 $\mathit{AD}$ 于点 $M$ ，连接 $\mathit{AG}$ ， $\mathit{DE}$ ， $\mathit{DF}$ ．

（1）求证： $\angle \mathit{GAD}+\angle \mathit{EDF}=180°$ ；

（2）若 $\angle \mathit{ACB}=45°$ ， $\mathit{AD}=4$ ， $\tan \angle \mathit{ABC}=2$ ，求 $\mathit{HF}$ 的长．

如图1，四边形 $\mathit{ABCD}$ 内接于 $\odot O$ ， $\mathit{AD}$ 为直径，点 $C$ 作 $\mathit{CE}\perp \mathit{AB}$ 于点 $E$ ，连接 $\mathit{AC}$ ．

（1）求证： $\angle \mathit{CAD}=\angle \mathit{ECB}$ ；

（2）若 $\mathit{CE}$ 是 $\odot O$ 的切线， $\angle \mathit{CAD}=30°$ ，连接 $\mathit{OC}$ ，如图2．

①请判断四边形 $\mathit{ABCO}$ 的形状，并说明理由；

②当 $\mathit{AB}=2$ 时，求 $\mathit{AD}$ ， $\mathit{AC}$ 与 $\stackrel{̂}{\mathit{CD}}$ 围成阴影部分的面积．

如图，已知 $\mathit{\Delta ABC}$内接于 $\odot O$，点 $C$在劣弧 $\mathit{AB}$上（不与点 $A$， $B$重合），点 $D$为弦 $\mathit{BC}$的中点， $\mathit{DE}\perp \mathit{BC}$， $\mathit{DE}$与 $\mathit{AC}$的延长线交于点 $E$，射线 $\mathit{AO}$与射线 $\mathit{EB}$交于点 $F$，与 $\odot O$交于点 $G$，设 $\angle \mathit{GAB}=\alpha$， $\angle \mathit{ACB}=\beta$， $\angle \mathit{EAG}+\angle \mathit{EBA}=\gamma$，

（1）点点同学通过画图和测量得到以下近似数据：

$\alpha$	$30°$	$40°$	$50°$	$60°$
$\beta$	$120°$	$130°$	$140°$	$150°$
$\gamma$	$150°$	$140°$	$130°$	$120°$

猜想： $\beta$关于 $\alpha$的函数表达式， $\gamma$关于 $\alpha$的函数表达式，并给出证明；

（2）若 $\gamma =135°$， $\mathit{CD}=3$， $\mathit{\Delta ABE}$的面积为 $\mathit{\Delta ABC}$的面积的4倍，求 $\odot O$半径的长．

如图，在矩形ABCD中，AB=3，BC=4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P作PE∥DC，交AC于点E，动点P、Q的运动速度是每秒1个单位长度，运动时间为t秒，当点P运动到点A时，P、Q两点同时停止运动．

（1）用含有t的代数式表示PE=           ；
（2）探究：当t为何值时，四边形PQBE为梯形？
（3）是否存在这样的点P和点Q，使△PQE为等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由．

（1）探究：如图1和2，四边形ABCD中，已知AB=AD，∠BAD=90°，点E、F分别在BC、CD上，∠EAF=45°．
①如图1，若∠B、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，则能证得EF=BE+DF，请写出推理过程；
②如图2，若∠B、∠D都不是直角，则当∠B与∠D满足数量关系          时，仍有EF=BE+DF；
（2）拓展：如图3，在△ABC中，∠BAC=90°，AB=AC=2，点D、E均在边BC上，且∠DAE=45°．若BD=1，求DE的长．

在矩形ABCD中，AB=a，AD=b，点M为BC边上一动点（点M与点B、C不重合），连接AM，过点M作MN⊥AM，垂足为M，MN交CD或CD的延长线于点N．

（1）求证：△CMN∽△BAM；
（2）设BM=x，CN=y，求y关于x的函数解析式．当x取何值时，y有最大值，并求出y的最大值；
（3）当点M在BC上运动时，求使得下列两个条件都成立的b的取值范围：①点N始终在线段CD上，②点M在某一位置时，点N恰好与点D重合．

如图①所示，已知A、B为直线a上两点，点C为直线a上方一动点，连接AC、BC，分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作D⊥a于点，过点E作E⊥a于点。

（1）如图②，当点E恰好在直线a上时，（此时E₁和E重合）。试说明D=AB；
（2）如图①中，当D、E两点都在直线a的上方时，试探求三条线段D、E、AB之间的数量关系，并说明理由。
（3）如图③，当点E在直线a的下方时，请直接写出三条线段D、E、AB之间的数量关系。（不需要证明）

已知：如图，在ABCD中，AE⊥BC，垂足为E，CE=CD，点F为CE的中点，点G为CD上的一点，连接DF、EG、AG，∠1=∠2。

（l）若CF=2，AE=3，求BE的长；
（2）求证：。