重庆市彭水县八年级下学期期末数学试卷
若分式 有意义,则a的取值范围是( )
有意义,则a的取值范围是( )
| A.a="0" | B.a="1" | C.a≠﹣1 | D.a≠0 |
若△ABC的周长是12cm,则△ABC三条中位线围成的三角形的周长为( )
| A.24cm | B.6cm | C.4cm | D.3cm |
如图,反比例函数 的图象经过点A(﹣1,﹣2).则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,﹣2).则当x>1时,函数值y的取值范围是( )
| A.y>1 | B.0<y<l | C.y>2 | D.0<y<2 |

已知如图,A是反比例函数 的图象上的一点,AB丄x轴于点B,且△ABO的面积是3,则k的值是( )
的图象上的一点,AB丄x轴于点B,且△ABO的面积是3,则k的值是( )
| A.3 | B.﹣3 | C.6 | D.﹣6 |

下面是四位同学解方程 过程中去分母的一步,其中正确的是( )
过程中去分母的一步,其中正确的是( )
| A.2+x=x﹣1 | B.2﹣x=1 |
| C.2+x=1﹣x | D.2﹣x=x﹣1 |
点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有( )
A.1个 B.2个 C.3个 D.4个
如图,菱形OABC的顶点B在y轴上,顶点C的坐标为(﹣2,1),若反比例函数 (x>0)的图象经过点A,则k的值为( )
(x>0)的图象经过点A,则k的值为( )
| A.2 | B.1 | C.﹣1 | D.﹣2 |

某中学足球队的18名队员的年龄情况如下表:
| 年龄(单位:岁) |
14 |
15 |
16 |
17 |
18 |
| 人数 |
3 |
6 |
4 |
4 |
1 |
则这些队员年龄的众数和中位数分别是( )
A.15,15 B.15,15.5 C.15,16 D.16,15
如图,△ABC中,AB=AC=13,BC=10,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
| A.16.5 | B.18 | C.23 | D.26 |

如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
| A.3 | B.4 | C.5 | D.6 |

今年年初,我国有的城市受雾霾天气的影响,PM2.5超标,对人体健康影响很大.PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,富含大量的有毒、有害物质.将0.0000025用科学记数法表示为 .
已知一个样本:﹣1,0,2,x,3,其平均数是2,则这个样本的方差s2= .(提示:方差公式为 .)
.)
一个水池装一个进水管和三个同样的出水管.先打开进水管,等水池储存一些水后,再打开出水管(进水管不关闭).若同时打开2个进水管,那么5小时后水池空;若同时打开3个出水管,则3小时后水池空.那么出水管比进水管晚开 小时.
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
为了改善生态环境,防止水土流失,某村计划在荒坡上种480棵树,由于青年志愿者的支援,每日比原计划多种 ,结果提前4天完成任务,原计划每天种多少棵树?
,结果提前4天完成任务,原计划每天种多少棵树?
春兰集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).
(1)利用图中提供的信息,在专业知识方面3人得分的极差是多少?在工作经验方面3人得分的众数是多少?在仪表形象方面谁最有优势?
(2)如果专业知识、工作经验、仪表形象三个方面的重要性之比为10:7:3,那么作为人事主管,你应该录用哪一位应聘者为什么?
(3)在(2)的条件下,你对落聘者有何建议?
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.求证:BE=AE+CD.(提示:解答需作辅助线哟!)
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
如图,在直角坐标系中,四边形OABC的OA,OC两边分别在x,y轴上,OA∥BC,BC=15cm,A点坐标为(16,0),C点坐标为(0,4).点P,Q分别从C,A同时出发,点P以2cm/s的速度由C向B运动,点Q以4cm/s的速度由A向O运动,当点Q到达点O时,点P也停止运动,设运动时间为t秒(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形?
(2)求当t为多少时?PQ所在直线将四边形OABC分成左右两部分的面积比为1:2;
(3)直接写出在(2)的情况下,直线PQ的函数关系式.
 的解为( )
的解为( )
 的值为0,则x= .
的值为0,则x= . 是反比例函数,且图象在第二、四象限内,则m的值是 .
是反比例函数,且图象在第二、四象限内,则m的值是 . ,则此平行四边形的面积为 .
,则此平行四边形的面积为 . ﹣|﹣2|+(2013﹣π)0﹣
﹣|﹣2|+(2013﹣π)0﹣ ﹣
﹣ .
.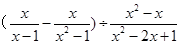 .其中x=2.
.其中x=2. 粤公网安备 44130202000953号
粤公网安备 44130202000953号