春兰集团对应聘者甲、乙、丙进行面试,并从专业知识、工作经验、仪表形象三方面给应聘者打分,每一方面满分20分,最后的打分制成条形统计图(如图).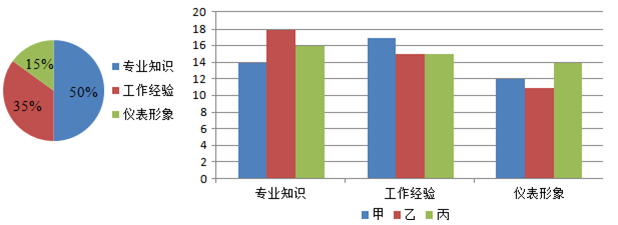
(1)利用图中提供的信息,在专业知识方面3人得分的极差是多少?在工作经验方面3人得分的众数是多少?在仪表形象方面谁最有优势?
(2)如果专业知识、工作经验、仪表形象三个方面的重要性之比为10:7:3,那么作为人事主管,你应该录用哪一位应聘者为什么?
(3)在(2)的条件下,你对落聘者有何建议?
相关知识点
推荐套卷
 ),它喜欢吃牛粪,它又会把吃剩的牛粪滚成牛粪球(
),它喜欢吃牛粪,它又会把吃剩的牛粪滚成牛粪球( )藏进仓库(
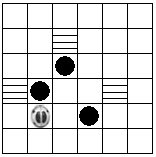
)藏进仓库( ).规定向左为L,向右为R,向上为U,向下D,如:L1表示向左平移一格,D2表示向下平移2格.例如:要把左图中的所有的牛粪球推到最近的仓库里,可以编写程序:L1-R1-U2-D3-R2-U1,小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试,可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.(只需写出一种可行的程序即可)
).规定向左为L,向右为R,向上为U,向下D,如:L1表示向左平移一格,D2表示向下平移2格.例如:要把左图中的所有的牛粪球推到最近的仓库里,可以编写程序:L1-R1-U2-D3-R2-U1,小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试,可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.(只需写出一种可行的程序即可)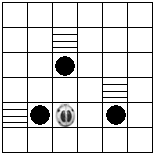


 ,-2012 这四个数使,则四次输出的结果依次为,,,。
,-2012 这四个数使,则四次输出的结果依次为,,,。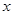 的方程
的方程 的解比关于
的解比关于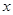 的方程
的方程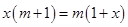 的解大
的解大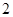 ,求出m的值并解这两个方程。
,求出m的值并解这两个方程。 粤公网安备 44130202000953号
粤公网安备 44130202000953号