如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),
(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线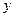 =-
=- +
+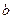 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与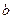 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.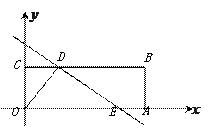
推荐套卷
如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),
(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线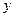 =-
=- +
+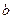 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与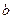 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.