初中数学垂径定理试题

如图，在Rt△ ABC中，∠ C＝90°，以 BC为直径的⊙ O交斜边 AB于点 M，若 H是 AC的中点，连接 MH．

（1）求证： MH为⊙ O的切线．

（2）若 $\mathit{MH}=\frac{3}{2},$ $\tan \angle \mathit{ABC}=\frac{3}{4}$ ，求⊙ O的半径．

（3）在（2）的条件下分别过点 A、 B作⊙ O的切线，两切线交于点 D， AD与⊙ O相切于 N点，过 N点作 NQ⊥ BC，垂足为 E，且交⊙ O于 Q点，求线段 NQ的长度．

如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O交于点F，连接DF、DC．已知 $\mathit{OA}＝\mathit{OB}，\mathit{CA}＝\mathit{CB}，\mathit{DE}＝10,\mathit{DF}＝6$．

（1）求证：①直线AB是⊙O的切线；② $\angle \mathit{FDC}＝\angle \mathit{EDC}$；

（2）求CD的长．

如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且 $\angle \mathit{DBC}＝\angle A$，连接OE延长与圆相交于点F，与BC相交于点C．

（1）求证：BC是⊙O的切线；

（2）若⊙O的半径为6， $\mathit{BC}＝8$，求弦BD的长．

如图，AB是圆O的直径，弦 $\mathit{CD}\perp \mathit{AB}$， $\angle \mathit{BCD}＝30°$， $\mathit{CD}=4\sqrt{3}$，则S_阴影＝（　　）

A．2πB． $\frac{8}{3}\pi$C． $\frac{4}{3}\pi$D． $\frac{3}{8}\pi$

如图， AB是⊙ O的弦， OC⊥ AB，交⊙ O于点 C，连接 OA， OB， BC，若∠ ABC＝20°，则∠ AOB的度数是（　　）

A．

40°

B．

50°

C．

70°

D．

80°

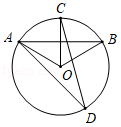
如图， AB是⊙ O的弦， OC⊥ AB交⊙ O于点 C，点 D是⊙ O上一点，∠ ADC＝30°，则∠ BOC的度数为（　　）

A．

30°

B．

40°

C．

50°

D．

60°

如图，在⊙ O中， B是⊙ O上的一点，∠ ABC＝120°，弦 AC＝2 $\mathrm{}\sqrt{3}$ ，弦 BM平分∠ ABC交 AC于点 D，连接 MA， MC．

（1）求⊙ O半径的长；

（2）求证： AB+ BC＝ BM．

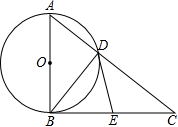
如图，在△ ABC中，∠ ABC＝90°，以 AB的中点 O为圆心， OA为半径的圆交 AC于点 D， E是 BC的中点，连结 DE、 OE．

（1）判断 DE与⊙ O的位置关系，并说明理由．

（2）求证： BC ²＝2 CD• OE．

已知⊙ O的半径为10，圆心 O到弦 AB的距离为5，则弦 AB所对的圆周角的度数是（　　）

A．

30°

B．

60°

C．

30°或150°

D．

60°或120°

如图，⊙ O为等腰三角形 ABC的外接圆， AB是⊙ O的直径， AB＝12， P为 $\stackrel{⏜}{\mathit{BC}}$ 上任意一点（不与点 B， C重合），直线 CP交 AB的延长线于点 Q，⊙ O在点 P处的切线 PD交 BQ于点 D，则下列结论：①若∠ PAB＝30°，则 $\stackrel{⏜}{\mathit{PB}}$ 的长为π；②若 PD∥ BC，则 AP平分∠ CAB；③若 PB＝ BD，则 PD＝6 $\sqrt{3}$ ；④无论点 P在 $\stackrel{⏜}{\mathit{BC}}$ 上的位置如何变化， CP• CQ＝108．其中正确结论的序号为 　　．

如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF＝∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG，已知DE＝4，AE＝8．

（1）求证：DF是⊙O的切线；

（2）求证：OC²＝OE•OP；

（3）求线段EG的长．

如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为G，OG：OC＝3：5，AB＝8．

（1）求⊙O的半径；

（2）点E为圆上一点，∠ECD＝15°，将 $\stackrel{̂}{\mathit{CE}}$沿弦CE翻折，交CD于点F，求图中阴影部分的面积．

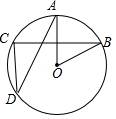
如图，在⊙ O中， OA⊥ BC，∠ AOB＝48°， D为⊙ O上一点，则∠ ADC的度数是（　　）

A．

24°

B．

42°

C．

48°

D．

12°

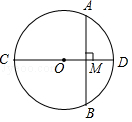
如图， CD为⊙ O的直径，弦 AB⊥ CD，垂足为 M，若 AB＝12， OM： MD＝5：8，则⊙ O的周长为（　　）

A．

26π

B．

13π

C．

$\frac{96\pi }{5}$

D．

$\frac{39\sqrt{10}\pi }{5}$

如图，将半圆形纸片折叠，使折痕 CD与直径 AB平行， $\stackrel{⏜}{\mathit{CD}}$ 的中点 P落在 OP上的点 P'处，且 OP'＝ $\frac{1}{3}$ OP，折痕 CD＝2 $\sqrt{3}$ ，则tan∠ COP的值为（　　）

A．

$\frac{6}{5}\sqrt{5}$

B．

$\frac{\sqrt{3}}{2}$

C．

$\frac{\sqrt{5}}{2}$

D．

$\frac{2}{5}\sqrt{5}$