如图, 是 的直径, 是 的弦, 交 于点 ,连接 , ,过点 作 ,垂足为 , .
(1)求证: ;
(2)点 在 的延长线上,连接 , .
①求证: 与 相切;
②当 , 时,直接写出 的长.

四边形 内接于 , 是 的直径, .
(1)如图1,求证 ;
(2)过点 作 的切线,交 延长线于点 (如图 .若 , ,求 的长.

如图,在平面直角坐标系中,点 在第一象限, 与 轴、 轴都相切,且经过矩形 的顶点 ,与 相交于点 .若 的半径为5,点 的坐标是 .则点 的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,为
的直径,
为
上一点,
与过
点的直线互相垂直,垂足为
,
平分
.
(1)求证:为
的切线.
(2)若,
,求
的半径.

定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形 中, , ,过点 作 垂线交 的延长线于点 ,且 ,证明:四边形 是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形 内接于 中, .求 的半径.

如图,在四边形 中, , , ,过点 的 与边 , 分别交于 , 两点. ,垂足为 , .连接 , , .

(1)若 ,试判断 的形状,并说明理由;
(2)若 ,求证: 与 相切于点 .
如图, 是 的直径, , 是 上两点,且 ,连接 , .过点 作 交 的延长线于点 .
(1)判定直线 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.
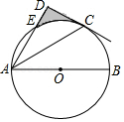
如图,在半径为3的 中, 是直径, 是弦, 是 的中点, 与 交于点 .若 是 的中点,则 的长是

| A. |
|
B. |
|
C. |
|
D. |
|
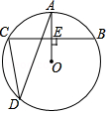
如图,点 , , , 在 上, ,垂足为 .若 , ,则
| A. |
2 |
B. |
4 |
C. |
|
D. |
|
如图, 的直径 , 是 的弦, ,垂足为 , ,则 的长为

| A. |
8 |
B. |
12 |
C. |
16 |
D. |
|