如图,已知⊙ O的直径为 AB, AC⊥ AB于点 A, BC与⊙ O相交于点 D,在 AC上取一点 E,使得 ED= EA.
(1)求证: ED是⊙ O的切线;
(2)当 OE=10时,求 BC的长.

如图,在平面直角坐标系中, O(0,0), A(0,﹣6), B(8,0)三点在⊙ P上, M为劣弧的 中点.
(1)求圆的半径及圆心 P的坐标;
(2)求证: AM是∠ OAB的平分线;
(3)连接 BM并延长交 y轴于点 N,求 N, M点的坐标.

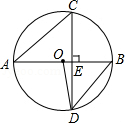
如图,线段 AB是⊙ O的直径,弦 CD⊥ AB,∠ CAB=40°,则∠ ABD与∠ AOD分别等于( )
| A. |
40°,80° |
B. |
50°,100° |
C. |
50°,80° |
D. |
40°,100° |
如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
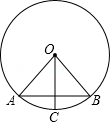
A.40°B.45°C.50°D.60°
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
如图,点 在以
在以 (南北方向)为直径的
(南北方向)为直径的 上,
上, ,
, 交
交 于点
于点 ,垂足为
,垂足为 ,
, ,弦
,弦 、
、 分别交
分别交 于点
于点 、
、 ,且
,且 .
.
(1)比较 与 的大小;
(2)若 ,求证:
,求证: ;
;
(3)设直线 、
、 相交所成的锐角为
相交所成的锐角为 ,试确定
,试确定 时,点
时,点 的位置.
的位置.

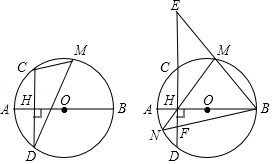
如图,线段 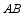 是
是 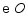 的直径,弦
的直径,弦 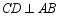 于点
于点 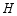 ,点
,点 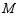 是
是 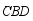 上任意一点,
上任意一点, 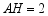 ,
, 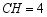 .
.
(1)求  的半径
的半径 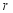 的长度;
的长度;
(2)求 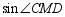 ;
;
(3)直线 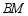 交直线
交直线 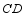 于点
于点 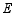 ,直线
,直线 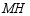 交
交 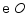 于点
于点 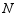 ,连接
,连接 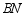 交
交 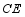 于点
于点 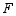 ,求
,求 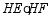 的值.
的值.
如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD,垂足为M点.
求证:(1)△ACO≌△BDO;(2)CE=DF.

如图,在  中,
中,  是直径,
是直径,  是弦,
是弦,  ,垂足为
,垂足为  ,连接
,连接  ,
,  ,
,  ,则下列说法中正确的是
,则下列说法中正确的是 


| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知⊙ O的半径为2, AB为直径, CD为弦. AB与 CD交于点 M,将 沿 CD翻折后,点 A与圆心 O重合,延长 OA至 P,使 AP= OA,连接 PC
(1)求 CD的长;
(2)求证: PC是⊙ O的切线;
(3)点 G为 的中点,在 PC延长线上有一动点 Q,连接 QG交 AB于点 E.交 于点 F( F与 B、 C不重合).问 GE• GF是否为定值?如果是,求出该定值;如果不是,请说明理由.

如图,以点 O为圆心的两个同心圆中,大圆的弦 AB是小圆的切线,点 P为切点, , OP=6,则劣弧 AB的长为 .

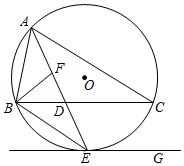
如图, 是 的外接圆,直线 与 相切于点 , ,连接 交 于点 .
(1)求证: 平分 ;
(2)若 的平分线 交 于点 ,且 , ,求 的长.