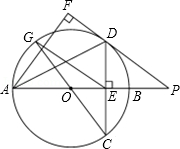
如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF＝∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG，已知DE＝4，AE＝8．
（1）求证：DF是⊙O的切线；
（2）求证：OC2＝OE•OP；
（3）求线段EG的长．
（不写
，其中x = -2，y = 
推荐套卷
如图，在⊙O中，直径AB垂直弦CD于E，过点A作∠DAF＝∠DAB，过点D作AF的垂线，垂足为F，交AB的延长线于点P，连接CO并延长交⊙O于点G，连接EG，已知DE＝4，AE＝8．
（1）求证：DF是⊙O的切线；
（2）求证：OC2＝OE•OP；
（3）求线段EG的长．
粤公网安备 44130202000953号