如图, 、 为 的直径,且 ,点 在 上,连接 、 , 于点 ,若 ,则 的度数是

A. B. C. D.
在平面直角坐标系中,点 的坐标为 ,以 为圆心的圆与 轴相切, 的弦 点在 点右侧)垂直于 轴,且 ,反比例函数 经过点 ,则 或 .
如图,在平面直角坐标系中, 与 轴相切于点 ,与 轴分别交于点 和点 ,则圆心 到坐标原点 的距离是
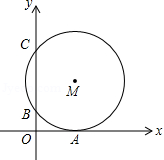
A.10B. C. D.
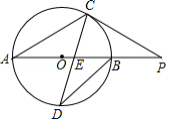
已知: 为 的直径,延长 到点 ,过点 作圆 的切线,切点为 ,连接 ,且 .
(1)求 的度数;
(2)若点 是弧 的中点,连接 交 于点 ,且 ,求 的面积. 取
如图,点 , , 均在 的正方形网格格点上,过 , , 三点的外接圆除经过 , , 三点外还能经过的格点数为 .

如图,在平面直角坐标系中, 的斜边 在 轴上,边 与 轴交于点 , 平分 交边 于点 ,经过点 、 、 的圆的圆心 恰好在 轴上, 与 轴相交于另一点 .
(1)求证: 是 的切线;
(2)若点 、 的坐标分别为 , ,求 的半径;
(3)试探究线段 、 、 三者之间满足的等量关系,并证明你的结论.

如图, 的直径 , 为 延长线上一点, 与 相切于点 ,过点 作弦 ,连接 .
(1)求证:点 为 的中点;
(2)若 ,求四边形 的面积.

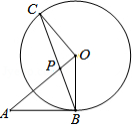
如图, 与 相切于点 , 为 的弦, , 与 相交于点 .
(1)求证: ;
(2)若 , ,求线段 的长.
如图, 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,求弦 的长.

如图1是一个用铁丝围成的篮筐,我们来仿制一个类似的柱体形篮筐.如图2,它是由一个半径为 、圆心角 的扇形 ,矩形 、 ,及若干个缺一边的矩形状框 、 、 、 , 围成,其中 、 、 在 上, 、 、 与 、 、 分别在半径 和 上, 、 、 、 和 、 分别在 和 上, 于 , 于 , , 、 、 、 依次等距离平行排放(最后一个矩形状框的边 与点 间的距离应不超过 ,
(1)求 的值;
(2)问: 与点 间的距离能否等于 ?如果能,求出这样的 的值,如果不能,那么它们之间的距离是多少?
