初中数学圆解答题

四年一度的国际数学家大会会标如图甲．它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．现有一张长为6.5cm、宽为2cm的纸片，如图乙，请你根据图甲的启示将它分割成6块，再拼合成一个正方形．（要求：先在图乙中画出分割线，再画出拼成的正方图甲形并标明相应数据）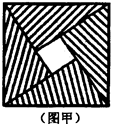

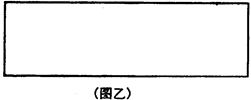
如图，网络中每个小正方形的边长为1，点的坐标为

画出直角坐标系（要求标出轴，轴和原点）并写出点的坐标；
以为基本图形，利用轴对称或旋转或平移设计一个图案，说明你的创意

如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为         .

）已知，如图，现有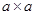、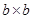的正方形纸片和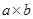的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．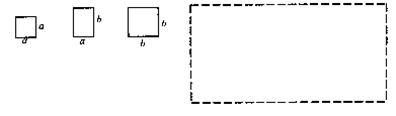

已知，正方形ABCD，点P在对角线BD上，连接AP、CP(如图①)

(1)求证：AP＝CP.
(2)将一直角三角板的直角顶点置于点P处并绕点P旋转，设两直角边分别交DC、BC于E、F，
a.若旋转到图②位置，使PE与PA在一直线上，求证：PF＝PA.
b.若旋转到图③位置且PD∶PB＝2∶3，求PE∶PF的值.

如图1，在Rt△ABC中，∠A＝90°，AB＝AC，BC＝4，另有一等腰梯形DEFG(GF∥DE)的底边DE与BC重合，两腰分别落在AB、AC上，且G、F分别是AB、AC的中点．
填空：GF的长度为________，等腰梯形DEFG的面积为________．
操作：固定△ABC，将等腰梯形DEFG以每秒1个单位的速度沿BC方向向右运动，直到点D与点C重合时停止．设运动时间为x秒，运动后的等腰梯形为DEF’G’(如图2)探究：在运动过程中，四边形BDG’G能否为菱形？若能，请求出此时x的值；若不能，请说明理由．

 

如图， AD∥BC，BD平分∠ABC，∠A=120°，∠C=60°，AB=CD=4cm，
求四边形ABCD的周长

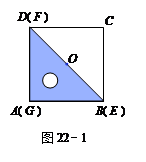
如图22－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．
如图22－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；
若三角尺GEF旋转到如图22－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．

类比学习：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位．用实数加法表示为 3+（）=1．
　　若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．
解决问题：
计算：{3，1}+{1，2}；{1，2}+{3，1}．
①动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C，再按照“平移量”{3，1}平移，最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
如图2，一艘船从码头O出发，先航行到湖心岛码头P（2，3），再从码头P航行到码头Q（5，2），最后回到出发点O. 请用“平移量”加法算式表示它的航行过程．

如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时的绿化面积．

如图，AB是⊙O的直径，点P是⊙O上的动点（P与A，B不重合），连结AP，PB，过点O分别作OE⊥AP于E，OF⊥BP于F．

若AB=12，当点P在⊙O上运动时，线段EF的长会不会改变．若会改变，请说明理由；若不会改变，请求出EF的长
若AP=BP，求证四边形OEPF是正方形

在图1至图3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．

如图1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，
求证：FM = MH，FM⊥MH
将图-1中的CE绕点C顺时针旋转一个锐角，得到图2，
求证：△FMH是等腰直角三角形
将图2中的CE缩短到图3的情况，△FMH还是等腰直角三角形吗？（不必
说明理由）

如图①，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE。(不需要证明)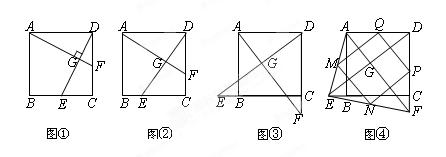

如图②，若点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF。则上面的结论①、②是否仍然成立？(请直接回答“成立”或“不成立”)
如图③，若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由。
如图④，在(2)的基础上，连接AE和EF，若点M、N、P、Q分别为AE、EF、FD、AD的中点，请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种？并写出证明过程。

如图，□ABCD的周长是36，且AB∶BC＝5∶4，对角线AC、BD相交于点O，且BD⊥AD，求OB的长。

如图，将矩形纸片沿对角线折叠，点落在点处，交于点，连结．求证：