如图,已知AD∥BC,AB=AD+BC,E是CD的中点,求∠AEB的度数。 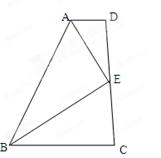
如图, 是同一直线上的三个点,四边形
是同一直线上的三个点,四边形 与四边形
与四边形 都是正方形,连结
都是正方形,连结 .
.观察图形,猜想
 与
与 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;若延长
 交
交 于点
于点 ,求证:
,求证: .
.
如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.求证:△BDF≌△CDE;
若AB=AC,求证:四边形BFCE是菱形.

(本题6分) 如图,在梯形 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
(1)
 与
与 有何等量关系?请说明理由;
有何等量关系?请说明理由;(2)当
 时,求证:平行四边形
时,求证:平行四边形 是矩形.
是矩形.
在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成 块;
请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成 块.
(画出图形不写画法和理由)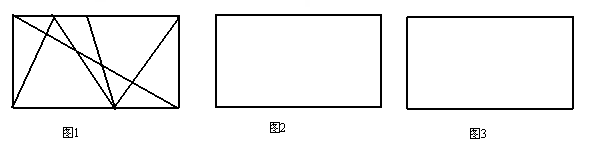
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
(本小题8分)
如图,已知平行四边形ABCD中,F、G是AB边上的两个点,且FC平分∠BCD,GD平分∠ADC,FC与GD相交于点E,求证:AF=GB.
(6分)如图,已知,四边形ABCD为梯形,分别过点A、D作底边BC的垂线,垂足分别为点E、F.四边形ADFE是何种特殊的四边形?请写出你的理由.
如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.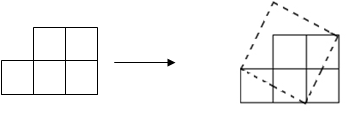

(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长
已知:如图,在平行四边形ABCD中,点E在AD上,连接BE,DF//BE交BC于点F,AF与BE交于点M,CE与DF交于点N. 
求证:四边形MFNE是平行四边形.
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,保留作图痕迹),并猜想BE与CD的关系:___________;你是通过证明_______________ 得到的。
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.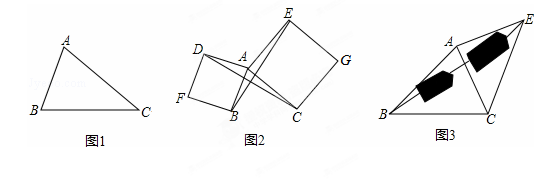
如图,正方形 中,
中,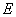 与
与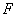 分别是
分别是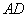 、
、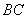 上一点.在
上一点.在
①  、 ②
、 ② 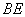 ∥
∥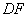 、 ③
、 ③ 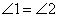 中,
中,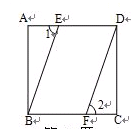
选择其中一个条件,证明
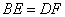
你选择的条件是 (只需填写序号)
如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
如图,在平行四边形ABCD中,AB在x轴上,D点y轴上, ,
, ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边 上一点,且
上一点,且 .点
.点 、
、 分别从
分别从 、
、 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿 、
、 向点
向点 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为 ,设运动时间为
,设运动时间为 秒。
秒。
求直线BC的解析式。
当
 为何值时,
为何值时, ?
?在(2)问条件下,⊙E与直线PF是否相切;如果相切,加以证明,并求出切点的坐标。如果不相切,说明理由。