浙江省杭州党湾镇初中八年级上学期期中考试数学试卷
下列长度的四根木棒中,能与长为4cm,9cm的两根木棒围成一个三角形的是( )
| A.4cm | B.5cm | C.9cm | D.14cm |
若a>b,则下列式子正确的是( )
| A.-2015a>-2015b | B.2015a<2015b | C.2015-a>2015-b | D.a-2015>b-2015 |
下列三条线段不能构成直角三角形的是( )
A.1、 、2 、2 |
B.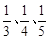 |
C.5、12、13 | D.9、40、41 |
若x,y满足|x-3|+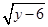 =0,则以x,y的值为两边长的等腰三角形的周长为( )
=0,则以x,y的值为两边长的等腰三角形的周长为( )
| A.12 | B.14 | C.15 | D.12或15 |
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
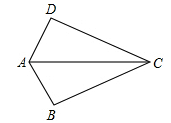
| A.CB=CD | B.∠BAC=∠DAC | C.∠BCA=∠DCA | D.∠B=∠D=90° |
下列说法正确的是( ).
| A.“邻补角相等吗?”是一个命题 |
| B.“同位角相等”的逆命题是假命题 |
| C.“相等的角是对顶角”是真命题 |
| D.“如果两条直线不相交那么一定平行”是真命题 |
已知ΔABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
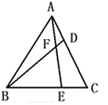
A.60° B.45° C.75° D.70°
已知三角形三边长分别为15、17、8,则此三角形的最长边上的高为( )
| A.17 | B. |
C.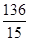 |
D.15 |
如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( )

| A.Rt△ACD≌Rt△BCE | B.OA=OB | C.E是AC的中点 | D.AE=BD |
如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与线段AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠AOF的度数是( )
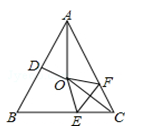
| A.105° | B.110° | C.115° | D.120° |
在直角三角形中,两条直角边的长分别是12和5,则斜边上的中线长是___________.
如图,△ABC中,∠BAC=100°,EF, MN分别为AB,AC的垂直平分线,如果BC="12" cm,那么△FAN的周长为 cm,∠FAN= .
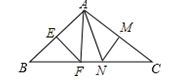
如图,△ABC的角平分线 CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②CA平分∠BCG;③∠ADC=∠GCD;④∠DFB=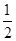 ∠CGE.
∠CGE.
其中正确的结论是_____________(填序号)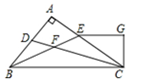
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,那么每个直角三角形的周长为 .

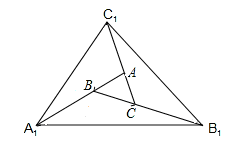
如图,△ABC的面积为1,第一次操作:分别延长AB,BC,CA,至点A1,B1,C1,使A1B=AB,B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,按此规律,要是得到的三角形的面积为38416,需要经过 次操作.
已知△ABC,用直尺和圆规做下列图形:(保留作图痕迹并写出结论)
(1)AC边上的中线;
(2)角平分线AM
如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.
如图 ,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:AC是BD的中垂线。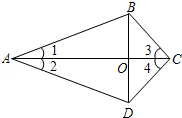
请判断下列命题的真假性,若是假命题请举反例说明。
(1)若a>b,则a2>b2;
(2)两个无理数的和仍是无理数;
(3)若三角形三边a,b,c满足(a-b)(b-c)(c-a)=0,则三角形是等边三角形;
(4)若三条线段a,b,c满足a+b>c,则这三条线段a,b,c能够组成三角形。
如图,在△ABC中,AD平分∠BAC.(1)若AC=BC,∠B:∠C=2:1,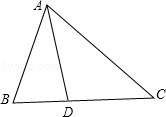
(1)写出图中的所有等腰三角形,并给予证明.
(2)若AB+BD=AC,求∠B:∠C的比值.
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,保留作图痕迹),并猜想BE与CD的关系:___________;你是通过证明_______________ 得到的。
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.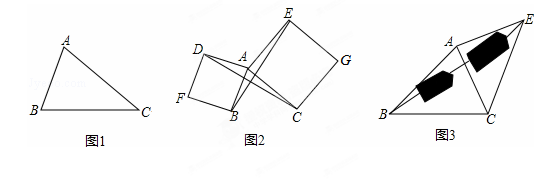
 粤公网安备 44130202000953号
粤公网安备 44130202000953号