初中数学圆试题

如图， $\mathit{ABCDEF}$为 $\odot O$的内接正六边形， $\mathit{AB}=a$，则图中阴影部分的面积是 $($　　 $)$

A． $\frac{\pi }{6}{a}^2$B． $(\frac{\pi }{6}-\frac{\sqrt{3}}{4})a^2$C． $\frac{\sqrt{3}}{4}{a}^2$D． $(\frac{\pi }{3}-\frac{\sqrt{3}}{4})a^2$

如图， $\mathit{AB}$为圆 $O$的直径， $C$为圆 $O$上一点， $D$为 $\mathit{BC}$延长线一点，且 $\mathit{BC}=\mathit{CD}$， $\mathit{CE}\perp \mathit{AD}$于点 $E$．

（1）求证：直线 $\mathit{EC}$为圆 $O$的切线；

（2）设 $\mathit{BE}$与圆 $O$交于点 $F$， $\mathit{AF}$的延长线与 $\mathit{CE}$交于点 $P$，已知 $\angle \mathit{PCF}=\angle \mathit{CBF}$， $\mathit{PC}=5$， $\mathit{PF}=4$，求 $\sin \angle \mathit{PEF}$的值．

如图， $\mathit{AB}$是半圆的直径， $\mathit{AC}$是一条弦， $D$是 $\stackrel{̂}{\mathit{AC}}$的中点， $\mathit{DE}\perp \mathit{AB}$于点 $E$且 $\mathit{DE}$交 $\mathit{AC}$于点 $F$， $\mathit{DB}$交 $\mathit{AC}$于点 $G$，若 $\frac{\mathit{EF}}{\mathit{AE}}=\frac{3}{4}$，则 $\frac{\mathit{CG}}{\mathit{GB}}=$　　．

刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积，设圆 $O$的半径为1，若用圆 $O$的外切正六边形的面积 $S$来近似估计圆 $O$的面积，则 $S=$　　．（结果保留根号）

在 $\mathit{\Delta ABC}$中，若 $O$为 $\mathit{BC}$边的中点，则必有： $A{B}^2+A{C}^2=2A{O}^2+2B{O}^2$成立．依据以上结论，解决如下问题：如图，在矩形 $\mathit{DEFG}$中，已知 $\mathit{DE}=4$， $\mathit{EF}=3$，点 $P$在以 $\mathit{DE}$为直径的半圆上运动，则 $P{F}^2+P{G}^2$的最小值为 $($　　 $)$

A． $\sqrt{10}$B． $\frac{19}{2}$C．34D．10

如图，过 $\odot O$外一点 $P$作 $\odot O$的切线 $\mathit{PA}$切 $\odot O$于点 $A$，连接 $\mathit{PO}$并延长，与 $\odot O$交于 $C$、 $D$两点， $M$是半圆 $\mathit{CD}$的中点，连接 $\mathit{AM}$交 $\mathit{CD}$于点 $N$，连接 $\mathit{AC}$、 $\mathit{CM}$．

（1）求证： $C{M}^2=\mathit{MN}\cdot \mathit{MA}$；

（2）若 $\angle P=30°$， $\mathit{PC}=2$，求 $\mathit{CM}$的长．

如图，在 $\odot O$中， $\mathit{AE}$是直径，半径 $\mathit{OC}$垂直于弦 $\mathit{AB}$于 $D$，连接 $\mathit{BE}$，若 $\mathit{AB}=2\sqrt{7}$， $\mathit{CD}=1$，则 $\mathit{BE}$的长是 $($　　 $)$

A．5B．6C．7D．8

已知圆锥的母线长为6，将其侧面沿着一条母线展开后所得扇形的圆心角为 $120°$，则该扇形的面积是 $($　　 $)$

A． $4\pi$B． $8\pi$C． $12\pi$D． $16\pi$

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$，以 $\mathit{AB}$为直径的 $\odot O$分别与 $\mathit{BC}$、 $\mathit{AC}$交于点 $D$、 $E$，过点 $D$作 $\mathit{DF}\perp \mathit{AC}$于点 $F$．

（1）若 $\odot O$的半径为3， $\angle \mathit{CDF}=15°$，求阴影部分的面积；

（2）求证： $\mathit{DF}$是 $\odot O$的切线；

（3）求证： $\angle \mathit{EDF}=\angle \mathit{DAC}$．

如图，以 $\text{Rt}\Delta \text{ABC}$的直角边 $\mathit{AB}$为直径作 $\odot O$交斜边 $\mathit{AC}$于点 $D$，过圆心 $O$作 $\mathit{OE}//\mathit{AC}$，交 $\mathit{BC}$于点 $E$，连接 $\mathit{DE}$．

（1）判断 $\mathit{DE}$与 $\odot O$的位置关系并说明理由；

（2）求证： $2D{E}^2=\mathit{CD}·\mathit{OE}$；

（3）若 $\tan C=\frac{4}{3}$， $\mathit{DE}=\frac{5}{2}$，求 $\mathit{AD}$的长．

已知 $\mathit{\Delta ABC}$的三边 $a$， $b$， $c$，满足 $a+b^2+|c-6|+28=4\sqrt{a-1}+10b$，则 $\mathit{\Delta ABC}$的外接圆半径 $=$　　．

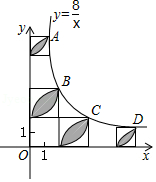
已知， $A$、 $B$、 $C$、 $D$是反比例函数 $y=\frac{8}{x}(x>0)$图象上四个整数点（横、纵坐标均为整数），分别过这些点向横轴或纵轴作垂线段，以垂线段所在的正方形（如图）的边长为半径作四分之一圆周的两条弧，组成四个橄榄形（阴影部分），则这四个橄榄形的面积总和是　　（用含 $\pi$的代数式表示）．

已知 $\odot O_1$的半径为 $3\mathit{cm}$， $\odot O_2$的半径为 $2\mathit{cm}$，圆心距 $O_1{O}_2=4\mathit{cm}$，则 $\odot O_1$与 $\odot O_2$的位置关系是 $($　　 $)$

A．外离B．外切C．相交D．内切

如图， $C$是 $\odot O$上一点，点 $P$在直径 $\mathit{AB}$的延长线上， $\odot O$的半径为3， $\mathit{PB}=2$， $\mathit{PC}=4$．

（1）求证： $\mathit{PC}$是 $\odot O$的切线．

（2）求 $\tan \angle \mathit{CAB}$的值．

如图， $\mathit{BC}$是 $\odot O$的直径， $A$是 $\odot O$上的一点， $\angle \mathit{OAC}=32°$，则 $\angle B$的度数是 $($　　 $)$

A． $58°$B． $60°$C． $64°$D． $68°$