如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
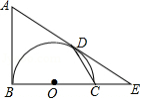
如图,已知 是等腰 的外接圆,点 是 上一点, 交 于点 ,若 , ,则 的长是

A.3B.2C.1D.1.2
四边形 的对角线交于点 ,有 , ,以 为直径的半圆过点 ,圆心为 .
(1)利用图1,求证:四边形 是菱形.
(2)如图2,若 的延长线与半圆相切于点 ,已知直径 .
①连接 ,求 的面积.
②求弧 的长.

足球射门,不考虑其他因素,仅考虑射点到球门 的张角大小时,张角越大,射门越好.如图的正方形网格中,点 , , , , 均在格点上,球员带球沿 方向进攻,最好的射点在
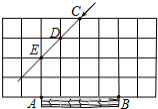
A.点 B.点 或点
C.线段 (异于端点) 上一点D.线段 (异于端点) 上一点
如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为 , , ,脸盆的最低点 到 的距离为 ,则该脸盆的半径为 .

如图, 是 的直径,点 、 在 上, , ,则 的度数是
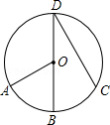
A. B. C. D.
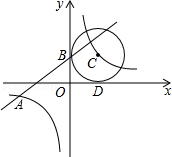
如图,已知一次函数 的图象与反比例函数 的图象交于点 ,且与 轴交于点 ,第一象限内点 在反比例函数 的图象上,且以点 为圆心的圆与 轴, 轴分别相切于点 ,
(1)求 的值;
(2)求一次函数的表达式;
(3)根据图象,当 时,写出 的取值范围.
把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是

A. B. C. D.
如图,已知四边形 内接于圆 ,连接 , , .
(1)求证: ;
(2)若圆 的半径为3,求 的长.

如图,圆 是 的外接圆, , ,过点 作圆 的切线,交 的延长线于点 ,则 的度数是
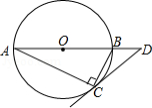
A. B. C. D.
如图,已知 是 的直径,点 在圆周上(不与 、 重合),点 在 的延长线上,连接 交 于点 ,若 ,则
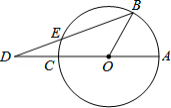
A. B. C. D.
如图,在 中, .
(1)作出经过点 ,圆心 在斜边 上且与边 相切于点 的 (要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)设(1)中所作的 与边 交于异于点 的另外一点 ,若 的直径为5, ;求 的长.(如果用尺规作图画不出图形,可画出草图完成(2)问)

已知圆锥的侧面积是 ,若圆锥底面半径为 ,母线长为 ,则 关于 的函数图象大致是
A. B.
B.
C.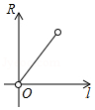 D.
D.