某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺 的0刻度固定在半圆的圆心 处,刻度尺可以绕点 旋转.从图中所示的图尺可读出 的值是

A. B. C. D.
如图, 是 的直径, 是 的切线,切点为 ,如果 ,则 的度数为
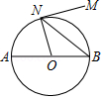
A. B. C. D.
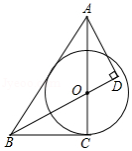
如图,在 中, 为 上一点,以点 为圆心, 为半径做圆,与 相切于点 ,过点 作 交 的延长线于点 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
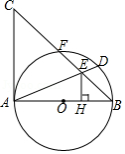
如图, 是 的 边上一点,连接 ,作 的外接圆,将 沿直线 折叠,点 的对应点 落在 上.
(1)求证: .
(2)若 , , ,求 的长.

小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若 所在的直线经过点 , ,小正六边形的面积为 ,则该圆的半径为 .

如图,公园内有一个半径为20米的圆形草坪, , 是圆上的点, 为圆心, ,从 到 只有路 ,一部分市民为走“捷径”,踩坏了花草,走出了一条小路 .通过计算可知,这些市民其实仅仅少走了 步(假设1步为0.5米,结果保留整数).(参考数据: , 取

如图,已知 为 直径, 是 的切线,连接 交 于点 ,取 的中点 ,连接 交 于点 ,过点 作 于 .
(1)求证: ;
(2)若 , ,求 和 的长.
如图, 是 的直径,弦 于 ,连接 ,过点 作 于 ,若 , ,则 的长度是
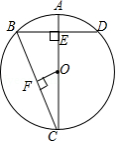
A. B. C. D.
如图, 是圆锥的母线, 为底面直径,已知 ,圆锥的侧面积为 ,则 的值为
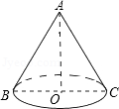
A. B. C. D.