如图,矩形纸片 , , ,点 、 分别在矩形的边 、 上,将矩形纸片沿直线 折叠,使点 落在矩形的边 上,记为点 ,点 落在 处,连接 ,交 于点 ,连接 .下列结论:①四边形 是菱形;②点 与点 重合时, ;③ 的面积 的取值范围是 .其中所有正确结论的序号是

| A. |
①②③ |
B. |
①② |
C. |
①③ |
D. |
②③ |
问题提出
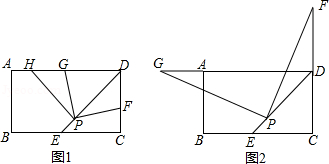
(1)如图1,在 中, , , 的平分线交 于点 .过点 分别作 , .垂足分别为 , ,则图1中与线段 相等的线段是 .
问题探究
(2)如图2, 是半圆 的直径, . 是 上一点,且 ,连接 , . 的平分线交 于点 ,过点 分别作 , ,垂足分别为 , ,求线段 的长.
问题解决
(3)如图3,是某公园内“少儿活动中心”的设计示意图.已知 的直径 ,点 在 上,且 . 为 上一点,连接 并延长,交 于点 .连接 , .过点 分别作 , ,垂足分别为 , .按设计要求,四边形 内部为室内活动区,阴影部分是户外活动区,圆内其余部分为绿化区.设 的长为 ,阴影部分的面积为 .
①求 与 之间的函数关系式;
②按照“少儿活动中心”的设计要求,发现当 的长度为 时,整体布局比较合理.试求当 时.室内活动区(四边形 的面积.

如图,在矩形 中, 是边 上一点, , ,垂足为 .将四边形 绕点 顺时针旋转 ,得到四边形 , 所在的直线分别交直线 于点 ,交直线 于点 ,交 于点 . 所在的直线分别交直线 于点 ,交直线 于点 ,连接 交 于点 .
(1)如图1,求证:四边形 是正方形;
(2)如图2,当点 和点 重合时.
①求证: ;
②若 , ,求线段 的长;
(3)如图3,若 交 于点 , ,求 的值.

如图,在矩形 中,点 在边 上, 与 关于直线 对称,点 的对称点 在边 上, 为 中点,连结 分别与 , 交于 , 两点.若 , ,则 的长为 , 的值为 .

如图①,在△ABC中, , , ,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为 时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.

如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 与矩形 重叠部分的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 的运动过程中,是否存在点 ,使 为等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.

如图,在 中, ,点 在 边上,过 , , 三点的 交 边于另一点 ,且 是 的中点, 是 的一条直径,连接 并延长交 边于 点.
(1)求证:四边形 为平行四边形;
(2)当 时,求 的值.

如图,在平面直角坐标系中,矩形 的边 在 轴上, 、 的长分别是一元二次方程 的两个根 , ,边 交 轴于点 ,动点 以每秒1个单位长度的速度,从点 出发沿折线段 向点 运动,运动的时间为 秒,设 的面积为 .
(1)求点 的坐标;
(2)求 关于 的函数关系式,并写出自变量的取值范围;
(3)在点 运动的过程中,是否存在点 ,使 是以 为腰的等腰三角形?若存在,直接写出点 的坐标;若不存在,请说明理由.
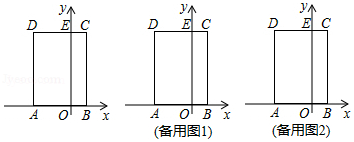
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线l:y=﹣x+7上时,记为点E,F,当点C的对应点落在边OA上时,记为点G.
(1)求点E,F的坐标;
(2)求经过E,F,G三点的抛物线的解析式;
(3)当点C的对应点落在直线l上时,求CD的长;
(4)在(2)中的抛物线上是否存在点P,使以E,F,P为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.

如图,矩形OABC的两边OA,OC分别在x轴和y轴的正半轴上,点B的坐标为( ),点D在CB上,且CD:DB=2:1,OB交AD于点E.平行于x轴的直线l从原点O出发,以每秒1个单位长度的速度沿y轴向上平移,到C点时停止;l与线段OB,AD分别相交与M,N两点,以MN为边作等边△MNP(点P在线段MN的下方).设直线l的运动时间为t(秒),△MNP与△OAB重叠部分的面积为S(平分单位).
(1)直接写出点E的坐标;
(2)求S与t的函数关系式;
(3)是否存在某一时刻t,使得 成立?若存在,请求出此时t的值;若不存在,请说明理由.

如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.
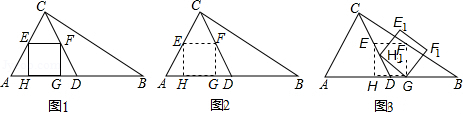
已知在矩形 中,
中, 的平分线
的平分线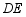 与
与 边所在的直线交于点
边所在的直线交于点 ,点
,点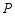 是线段
是线段 上一定点(其中
上一定点(其中
(1)如图1,若点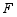 在
在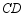 边上(不与
边上(不与 重合),将
重合),将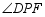 绕点
绕点 逆时针旋转
逆时针旋转 后,角的两边
后,角的两边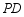 、
、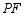 分别交射线
分别交射线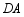 于点
于点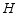 、
、 .
.
①求证: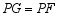 ; ②探究:
; ②探究: 、
、 、
、 之间有怎样的数量关系,并证明你的结论.
之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点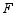 在
在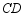 的延长线上(不与
的延长线上(不与 重合),过点
重合),过点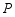 作
作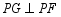 ,交射线
,交射线 于点
于点 ,你认为(1)中
,你认为(1)中 、
、 、
、 之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
如图,在矩形 中, , ,点 在线段 上运动(含 、 两点),连接 ,以点 为中心,将线段 逆时针旋转 到 ,连接 ,则线段 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
3 |
如图所示,在矩形纸片 中, , ,点 、 分别是矩形的边 、 上的动点,将该纸片沿直线 折叠.使点 落在矩形边 上,对应点记为点 ,点 落在 处,连接 、 、 , 与 交于点 .则下列结论成立的是
① ;
②当点 与点 重合时, ;
③ 的面积 的取值范围是 ;
④当 时, .

| A. |
①③ |
B. |
③④ |
C. |
②③ |
D. |
②④ |