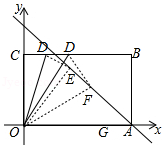
如图，在矩形OABC纸片中，OA＝7，OC＝5，D为BC边上动点，将△OCD沿OD折叠，当点C的对应点落在直线l：y＝﹣x+7上时，记为点E，F，当点C的对应点落在边OA上时，记为点G．
（1）求点E，F的坐标；
（2）求经过E，F，G三点的抛物线的解析式；
（3）当点C的对应点落在直线l上时，求CD的长；
（4）在（2）中的抛物线上是否存在点P，使以E，F，P为顶点的三角形是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．
相关试题
如图，
中，
、
两点在
轴的上方，点
的坐标是(-1，0)．以点为位似中心，在轴的下方作的位似图形
，并把的边长放大到原来的2倍．设点的对应点
的横坐标是2，求点的横坐标
心理学家经过调查发现，某班级的学生对概念的接受能力
与提出概念所用的时间
（单位：分）之间满足函数关系：
．其中，值越大，表示接受能力越强．
（1）第10分钟时，学生的接受能力是多少？
（2）第几分时，学生的接受能力最强？
（3）在什么范围内，学生的接受能力逐步增强？
是⊙O的直径，
是弦，
，延长
，使得
．
是⊙O的切线；
，求
的长下图是由转盘和指针组成的装置
、
，两个转盘分别被分成三个面积相等的扇形. 装置上的数字分别是1，6，8，装置上的数字分别是4，5，7. 这两个装置除了表面数字不同外，其他构造完全相同. 现在你和另外一个同学分别同时用力转动装置、中的指针，如果我们规定指针停留在较大数字的一方获胜（若指针恰好停留在分界线上，则重新转动
一次，直到指针停留在某一数字为止），那么你选择的装置是，请说明理由．
处时的线长为20米，此时小明正好站在A处，并测得
，牵引底端
离地面1.5米，求此时风筝离地面的高度．
相关知识点
推荐套卷
粤公网安备 44130202000953号