如图,在菱形中,连结
、
交于点
,过点
作
于点
,以点
为圆心,
为半径的半圆交
于点
.
①求证:是
的切线.
②若且
,求图中阴影部分的面积.
③在②的条件下,是线段
上的一动点,当
为何值时,
的值最小,并求出最小值.

如图,矩形的顶点
,
分别在菱形
的边
,
上,顶点
,
在菱形
的对角线
上.
(1)求证:;
(2)若为
中点,
,求菱形
的周长.

在图1,2,3中,已知,
,点
为线段
上的动点,连接
,以
为边向上作菱形
,且
.
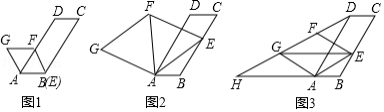
(1)如图1,当点与点
重合时,
;
(2)如图2,连接.
①填空:
(填“
”,“
“,“
”
;
②求证:点在
的平分线上;
(3)如图3,连接,
,并延长
交
的延长线于点
,当四边形
是平行四边形时,求
的值.
如图,在中,
,
,以
为直径的半圆
交
于点
,点
是
上不与点
,
重合的任意一点,连接
交
于点
,连接
并延长交
于点
.
(1)求证:;
(2)填空:
①若,且点
是
的中点,则
的长为 ;
②取的中点
,当
的度数为 时,四边形
为菱形.

如图,为半圆
的直径,点
为半圆上任一点.
(1)若,过点
作半圆
的切线交直线
于点
.求证:
;
(2)若,过点
作
的平行线交半圆
于点
.当以点
,
,
,
为顶点的四边形为菱形时,求
的长.

如图,在菱形中,对角线
与
相交于点
,
,
,点
从点
出发,沿
以每秒2个单位长度的速度向终点
运动,当点
不与点
重合时,过点
作
于点
,作
交
于点
,过点
作
交
(或
的延长线)于点
,得到矩形
,设点
运动的时间为
秒
(1)求线段的长(用含
的代数式表示);
(2)求点与点
重合时
的值;
(3)设矩形与菱形
重叠部分图形的面积与
平方单位,求
与
之间的函数关系式;
(4)矩形的对角线
与
相交于点
,当
时,
的值为 ;当
时,
的值为 .
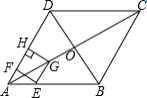
如图,在菱形中,
为对角线,点
,
分别在
,
上,
,连接
.
(1)求证:;
(2)延长交
的延长线于点
,连接
交
于点
.若
,
,求
的长.

如图,菱形的对角线
,
相交于点
,
是
的中点,点
,
在
上,
,
.
(1)求证:四边形是矩形;
(2)若,
,求
和
的长.

(年云南省曲靖市)如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是 ,tanα=
,tanα= ,求四边形OBEC的面积.
,求四边形OBEC的面积.
(年新疆、生产建设兵团)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
(1)如图①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)