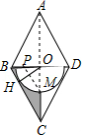
如图,在菱形中,连结、交于点,过点作于点,以点为圆心,为半径的半圆交于点.
①求证:是的切线.
②若且,求图中阴影部分的面积.
③在②的条件下,是线段上的一动点,当为何值时,的值最小,并求出最小值.
相关知识点
推荐套卷
如图,在菱形中,连结、交于点,过点作于点,以点为圆心,为半径的半圆交于点.
①求证:是的切线.
②若且,求图中阴影部分的面积.
③在②的条件下,是线段上的一动点,当为何值时,的值最小,并求出最小值.
