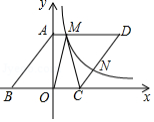
如图,菱形 的顶点 在 轴正半轴上,边 在 轴上,且 , ,反比例函数 的图象分别与 , 交于点 、点 ,点 的坐标是 ,连接 , .
(1)求反比例函数的解析式;
(2)求证: 是等腰三角形.
如图1,以 的较短边 为一边作菱形 ,使点 落在边 上,连接 ,交 于点 .
(1)猜想 与 的数量关系,并说明理由;
(2)延长 、 交于点 ,其他条件不变:
①如图2,若 ,求 的值;
②如图3,若
,直接写出
的值(用含
的三角函数表示)
菱形 中、 ,点 为射线 上的动点,作射线 与直线 相交于点 ,将射线 绕点 逆时针旋转 ,得到射线 ,射线 与直线 相交于点 .
(1)如图①,点 与点 重合时,点 , 分别在线段 , 上,请直接写出 , , 三条段段之间的数量关系;
(2)如图②,点 在 的延长线上,且 , , 分别在线段 的延长线和线段 的延长线上,请写出 , , 三条线段之间的数量关系,并说明理由;
(3)点 在线段 上,若 , ,当 时,请直接写出 的长.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

如图,在平面直角坐标系中,菱形 的边 在 轴上,反比例函数 的图象经过菱形对角线的交点 ,且与边 交于点 ,点 的坐标为 .
(1)求反比例函数的表达式;
(2)求点 的坐标.

如图,已知 中, ,把 绕 点沿顺时针方向旋转得到 ,连接 , 交于点 .
(1)求证: ;
(2)若 , ,当四边形 是菱形时,求 的长.

菱形 的周长为8, ,以 为腰,在菱形外作底角是 的等腰 ,连接 , .请画出图形,并直接写出 的面积.
如图,菱形 的边 在 轴上,点 的坐标为 ,点 在反比例函数 的图象上,直线 经过点 ,与 轴交于点 ,连接 , .
(1)求 , 的值;
(2)求 的面积.

如图,菱形 中,作 、 ,分别交 、 的延长线于点 、 .
(1)求证: ;
(2)若点 恰好是 的中点, ,求 的值.

如图,在菱形 中,点 在对角线 上,且 , 是 的外接圆.
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
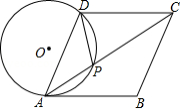
如图,在菱形 ABCD中, G是 BD上一点,连接 CG并延长交 BA的延长线于点 F,交 AD于点 E.
(1)求证: AG= CG.
(2)求证: AG 2= GE• GF.
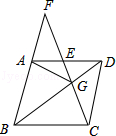
如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
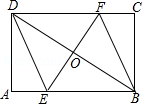
如图, BD是菱形 ABCD的对角线,∠ CBD=75°,
(1)请用尺规作图法,作 AB的垂直平分线 EF,垂足为 E,交 AD于 F;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接 BF,求∠ DBF的度数.
(1)【探究发现】
如图1,∠ EOF的顶点 O在正方形 ABCD两条对角线的交点处,∠ EOF=90°,将∠ EOF绕点 O旋转,旋转过程中,∠ EOF的两边分别与正方形 ABCD的边 BC和 CD交于点 E和点 F(点 F与点 C, D不重合).则 CE, CF, BC之间满足的数量关系是 .
(2)【类比应用】
如图2,若将(1)中的"正方形 ABCD"改为"∠ BCD=120°的菱形 ABCD",其他条件不变,当∠ EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)【拓展延伸】
如图3,∠ BOD=120°, OD= , OB=4, OA平分∠ BOD, AB= ,且 OB>2 OA,点 C是 OB上一点,∠ CAD=60°,求 OC的长.
