初中数学平行四边形的性质试题

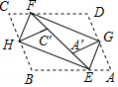
如图，平行四边形纸片 $\mathit{ABCD}$的边 $\mathit{AB}$， $\mathit{BC}$的长分别是 $10\mathit{cm}$和 $7.5\mathit{cm}$，将其四个角向内对折后，点 $B$与点 $C$重合于点 $C^{\text{'}}$，点 $A$与点 $D$重合于点 $A\text{'}$．四条折痕围成一个“信封四边形” $\mathit{EHFG}$，其顶点分别在平行四边形 $\mathit{ABCD}$的四条边上，则 $\mathit{EF}=$　　 $\mathit{cm}$．

如图，在 $▱\mathit{ABCD}$中，已知 $\mathit{AD}>\mathit{AB}$．

（1）实践与操作：作 $\angle \mathit{BAD}$的平分线交 $\mathit{BC}$于点 $E$，在 $\mathit{AD}$上截取 $\mathit{AF}=\mathit{AB}$，连接 $\mathit{EF}$；（要求：尺规作图，保留作图痕迹，不写作法）

（2）猜想并证明：猜想四边形 $\mathit{ABEF}$的形状，并给予证明．

如图，在 $▱\mathit{ABCD}$中， $\mathit{AC}$是对角线， $\mathit{BE}\perp \mathit{AC}$， $\mathit{DF}\perp \mathit{AC}$，垂足分别为点 $E$， $F$，求证： $\mathit{AE}=\mathit{CF}$．

已知：如图，四边形 $\mathit{ABCD}$是平行四边形，延长 $\mathit{BA}$至点 $E$，使 $\mathit{AE}+\mathit{CD}=\mathit{AD}$．连接 $\mathit{CE}$，求证： $\mathit{CE}$平分 $\angle \mathit{BCD}$．

平行四边形 $\mathit{ABCD}$中， $\mathit{AC}$、 $\mathit{BD}$是两条对角线，现从以下四个关系① $\mathit{AB}=\mathit{BC}$；② $\mathit{AC}=\mathit{BD}$；③ $\mathit{AC}\perp \mathit{BD}$；④ $\mathit{AB}\perp \mathit{BC}$中随机取出一个作为条件，即可推出平行四边形 $\mathit{ABCD}$是菱形的概率为 $($　　 $)$

A． $\frac{1}{4}$B． $\frac{1}{2}$C． $\frac{3}{4}$D．1

平行四边形ABCD的两个顶点A、C在反比例函数 $y=\frac{\text{k}}{\text{x}}(k\ne 0)$图象上，点B、D在x轴上，且B、D两点关于原点对称，AD交y轴于P点

（1）已知点A的坐标是（2，3），求k的值及C点的坐标；

（2）在（1）的条件下，若△APO的面积为2，求点D到直线AC的距离．

如图，在 $▱\mathit{ABCD}$中， $\mathit{AD}=12$，以 $\mathit{AD}$为直径的 $\odot O$与 $\mathit{BC}$相切于点 $E$，连接 $\mathit{OC}$．若 $\mathit{OC}=\mathit{AB}$，则 $▱\mathit{ABCD}$的周长为 　　．

如图，在 $▱\mathit{ABCD}$中， $\mathit{AE}\perp \mathit{BC}$， $\mathit{AF}\perp \mathit{CD}$，垂足分别为 $E$， $F$，且 $\mathit{BE}=\mathit{DF}$．

（1）求证： $▱\mathit{ABCD}$是菱形；

（2）若 $\mathit{AB}=5$， $\mathit{AC}=6$，求 $▱\mathit{ABCD}$的面积．

如图，四边形 $\mathit{ABCD}$ 为平行四边形，连接 $\mathit{AC}$ ，且 $\mathit{AC}=2\mathit{AB}$ ．请用尺规完成基本作图：作出 $\angle \mathit{BAC}$ 的角平分线与 $\mathit{BC}$ 交于点 $E$ ．连接 $\mathit{BD}$ 交 $\mathit{AE}$ 于点 $F$ ，交 $\mathit{AC}$ 于点 $O$ ，猜想线段 $\mathit{BF}$ 和线段 $\mathit{DF}$ 的数量关系，并证明你的猜想．（尺规作图保留作图痕迹，不写作法）

如图是由边长为1的小正方形构成的 $6\times 4$ 的网格，点 $A$ ， $B$ 均在格点上．

（1）在图1中画出以 $\mathit{AB}$ 为边且周长为无理数的 $▱\mathit{ABCD}$ ，且点 $C$ 和点 $D$ 均在格点上（画出一个即可）．

（2）在图2中画出以 $\mathit{AB}$ 为对角线的正方形 $\mathit{AEBF}$ ，且点 $E$ 和点 $F$ 均在格点上．

如图，在平行四边形 $\mathit{ABCD}$ 中， $E$ 为 $\mathit{DC}$ 边的中点，连接 $\mathit{AE}$ ，若 $\mathit{AE}$ 的延长线和 $\mathit{BC}$ 的延长线相交于点 $F$ ．

（1）求证： $\mathit{BC}=\mathit{CF}$ ；

（2）连接 $\mathit{AC}$ 和 $\mathit{BE}$ 相交于点为 $G$ ，若 $\mathit{\Delta GEC}$ 的面积为2，求平行四边形 $\mathit{ABCD}$ 的面积．

如图， $\mathit{AB}$ 是 $\odot O$ 的直径，过点 $A$ 作 $\odot O$ 的切线 $\mathit{AC}$ ，点 $P$ 是射线 $\mathit{AC}$ 上的动点，连接 $\mathit{OP}$ ，过点 $B$ 作 $\mathit{BD}//\mathit{OP}$ ，交 $\odot O$ 于点 $D$ ，连接 $\mathit{PD}$ ．

（1）求证： $\mathit{PD}$ 是 $\odot O$ 的切线；

（2）当四边形 $\mathit{POBD}$ 是平行四边形时，求 $\angle \mathit{APO}$ 的度数．

如图，在 $▱\mathit{ABCD}$ 中， $E$ 为 $\mathit{BC}$ 的中点，连接 $\mathit{AE}$ 并延长交 $\mathit{DC}$ 的延长线于点 $F$ ，连接 $\mathit{BF}$ ， $\mathit{AC}$ ，若 $\mathit{AD}=\mathit{AF}$ ，求证：四边形 $\mathit{ABFC}$ 是矩形．

如图， $E$是 $▱\mathit{ABCD}$的边 $\mathit{CD}$的中点，延长 $\mathit{AE}$交 $\mathit{BC}$的延长线于点 $F$．

（1）求证： $\mathit{\Delta ADE}\cong \mathit{\Delta FCE}$．

（2）若 $\angle \mathit{BAF}=90°$， $\mathit{BC}=5$， $\mathit{EF}=3$，求 $\mathit{CD}$的长．

已知，如图1，在 $▱\mathit{ABCD}$中，点 $E$是 $\mathit{AB}$中点，连接 $\mathit{DE}$并延长，交 $\mathit{CB}$的延长线于点 $F$．

（1）求证： $\mathit{\Delta ADE}\cong \mathit{\Delta BFE}$；

（2）如图2，点 $G$是边 $\mathit{BC}$上任意一点（点 $G$不与点 $B$、 $C$重合），连接 $\mathit{AG}$交 $\mathit{DF}$于点 $H$，连接 $\mathit{HC}$，过点 $A$作 $\mathit{AK}//\mathit{HC}$，交 $\mathit{DF}$于点 $K$．

①求证： $\mathit{HC}=2\mathit{AK}$；

②当点 $G$是边 $\mathit{BC}$中点时，恰有 $\mathit{HD}=n\cdot \mathit{HK}(n$为正整数），求 $n$的值．