初中数学平行四边形的性质试题

如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

（1）求证： $\mathit{BE}＝\mathit{CD}$；

（2）连接BF，若 $\mathit{BF}\perp \mathit{AE}$， $\angle \mathit{BEA}＝60°$， $\mathit{AB}＝4$求平行四边形ABCD的面积．

如图所示，点E，F是平行四边形ABCD对角线BD上的点， $\mathit{BF}＝\mathit{DE}$，求证：AE＝CF．

如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D₁，折痕为EF，若 $\angle \mathit{BAE}＝55°$，则 $\angle D_1\mathit{AD}＝$　　．

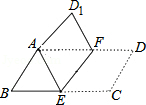
已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线BD作垂线，垂足分别为点E、F，点O为AC的中点．

（1）当点P与点O重合时如图1，易证 $\mathit{OE}＝\mathit{OF}$（不需证明）

（2）直线BP绕点B逆时针方向旋转，当 $\angle \mathit{OFE}＝30°$时，如图2、图3的位置，猜想线段CF、AE、OE之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．

已知：在平行四边形ABCD中，点E在直线AD上， $\mathit{AE}=\frac{1}{3}\mathit{AD}$，连接CE交BD于点F，则 $\mathit{EF}：\mathit{FC}$的值是　　．

已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线BD作垂线，垂足分别为点E、F，点O为AC的中点．

（1）当点P与点O重合时如图1，易证 $\mathit{OE}＝\mathit{OF}$（不需证明）

（2）直线BP绕点B逆时针方向旋转，当 $\angle \mathit{OFE}＝30°$时，如图2、图3的位置，猜想线段CF、AE、OE之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．

如图，若以平行四边形一边 AB为直径的圆恰好与对边 CD相切于点 D，则∠ C＝ 　　度．

在△ABC中， $\mathit{AB}＝6，$ $\mathit{AC}＝8，$ $\mathit{BC}＝10$，D是△ABC内部或BC边上的一个动点（与B、C不重合），以D为顶点作△DEF，使△DEF∽△ABC（相似比k＞1），EF∥BC．

（1）求∠D的度数；

（2）若两三角形重叠部分的形状始终是四边形AGDH．

①如图1，连接GH、AD，当 $\mathit{GH}\perp \mathit{AD}$时，请判断四边形AGDH的形状，并证明；

②当AGDH的面积最大时，过A作 $\mathit{AP}\perp \mathit{EF}$于P，且 $\mathit{AP}＝\mathit{AD}$，求k的值．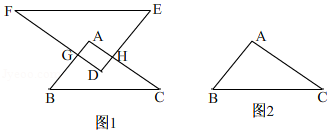

在▱ABCD中， $\mathit{AD}＝8$，AE平分 $\angle \mathit{BAD}$交BC于点E，DF平分∠ADC交BC于点F，且 $\mathit{EF}＝2$，则AB的长为（　　）

A．3B．5C．2或3D．3或5

如图，在▱ABCD中， $\mathit{AB}＞\mathit{AD}$，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于 $\frac{1}{2}$EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（　　）

A． $\mathit{AG}\mathit{平分}\angle \mathit{DAB}$B． $\mathit{AD}＝\mathit{DH}$C． $\mathit{DH}＝\mathit{BC}$D． $\mathit{CH}＝\mathit{DH}$

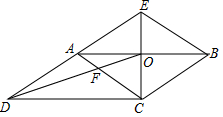
如图， CE是▱ ABCD的边 AB的垂直平分线，垂足为点 O， CE与 DA的延长线交于点 E．连接 AC， BE， DO， DO与 AC交于点 F，则下列结论：

①四边形 ACBE是菱形；

②∠ ACD＝∠ BAE；

③ AF： BE＝2：3；

④ S _{四边形 AFOE}： S _{△ COD}＝2：3．

其中正确的结论有 　　．（填写所有正确结论的序号）

如图，在▱ ABCD中，∠ BDC＝47°42′，依据尺规作图的痕迹，计算α的度数是（　　）

A．

67°29′

B．

67°9′

C．

66°29′

D．

66°9′

已知： AC是▱ ABCD的对角线．

（1）用直尺和圆规作出线段 AC的垂直平分线，与 AD相交于点 E，连接 CE．（保留作图痕迹，不写作法）；

（2）在（1）的条件下，若 AB＝3， BC＝5，求△ DCE的周长．

如图，△ ABC中， D是 BC边上一点， E是 AD的中点，过点 A作 BC的平行线交 BE的延长线于 F，且 AF＝ CD，连接 CF．

（1）求证：△ AEF≌△ DEB；

（2）若 AB＝ AC，试判断四边形 ADCF的形状，并证明你的结论．

如图，▱ ABCD的对角线 AC、 BD交于点 O， DE平分∠ ADC交 AB于点 E，∠ BCD＝60°， AD＝ $\frac{1}{2}$ AB，连接 OE．下列结论：① S _{▱ ABCD}＝ AD• BD；② DB平分∠ CDE；③ AO＝ DE；④ S _{△ ADE}＝5 S _{△ OFE}，其中正确的个数有（　　）

A．

1个

B．

2个

C．

3个

D．

4个